Предмет: Геометрия,
автор: aberdyeva78
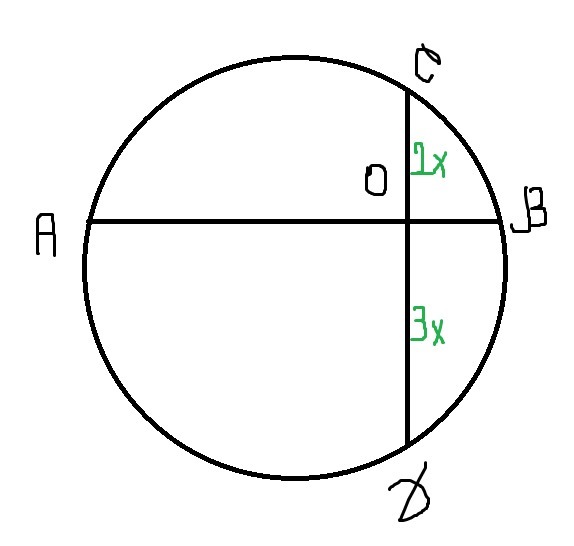
В окружности проведены две пересекаюшиеся ходы АВ =7 , СД =5 .Точка их пересечения делит СД в отношении 2:3 .В каком отношении эта точка делит ходу АВ? В ответе укажите отношение меньшего к большему отрезка.
Ответы
Автор ответа:
1
1:6
CO:DO=2x:3x
x=1 CO=2 DO=3
AO:BO=CO*DO=2*3=6
AO+BO=AB=7
Автор ответа:
1
18_03_09_Задание № 6:
В окружности проведены две пересекающиеся хорды AB=7, CD=5. Точка их пересечения делит CD в отношении 2:3. В каком отношении эта точка делит хорду AB? (В ответе укажите отношение меньшего отрезка к большему).
РЕШЕНИЕ: Пусть О - точка пересечения хорд. Тогда, CO/DO=2/3=2x/3x.
Выразим CD: СD=CO+DO=2x+3x=5x=5, значит х=1. CO=2, DO=3
По теореме о пересекающихся хордах: АO*BO=CO*DO=2*3=6
С другой стороны АО+ВО=АВ=7. Выразим АО=7-ВО и подставим в теорему:
(7-ВО)*BO=6
BO^2-7BO+6=0
(BO-1)(BO-6)=0
ВО=1, тогда АО=6
или ВО=6, тогда АО=1
В любом случае отношение меньшей части к большей равно 1:6.
ОТВЕТ: 1:6
Приложения:
Похожие вопросы
Предмет: Математика,
автор: zamuruevaluba
Предмет: Алгебра,
автор: 66E6RTRBT
Предмет: Информатика,
автор: deckwine
Предмет: Математика,
автор: somayaaJJJJJh