Предмет: Алгебра,
автор: Profit228
Найдите производную функции
Приложения:
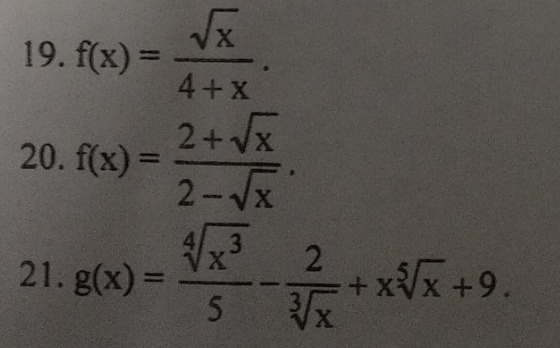
Ответы
Автор ответа:
0
19. f'(x) =
20. f'(x) =
21.-
Похожие вопросы
Предмет: Геометрия,
автор: dilmurodk040
Предмет: Русский язык,
автор: almuradlikamila
Предмет: Русский язык,
автор: zablicevavika1
Предмет: Алгебра,
автор: Аноним