Предмет: Алгебра,
автор: FanGen
Пожалуйста помогите решить
Приложения:
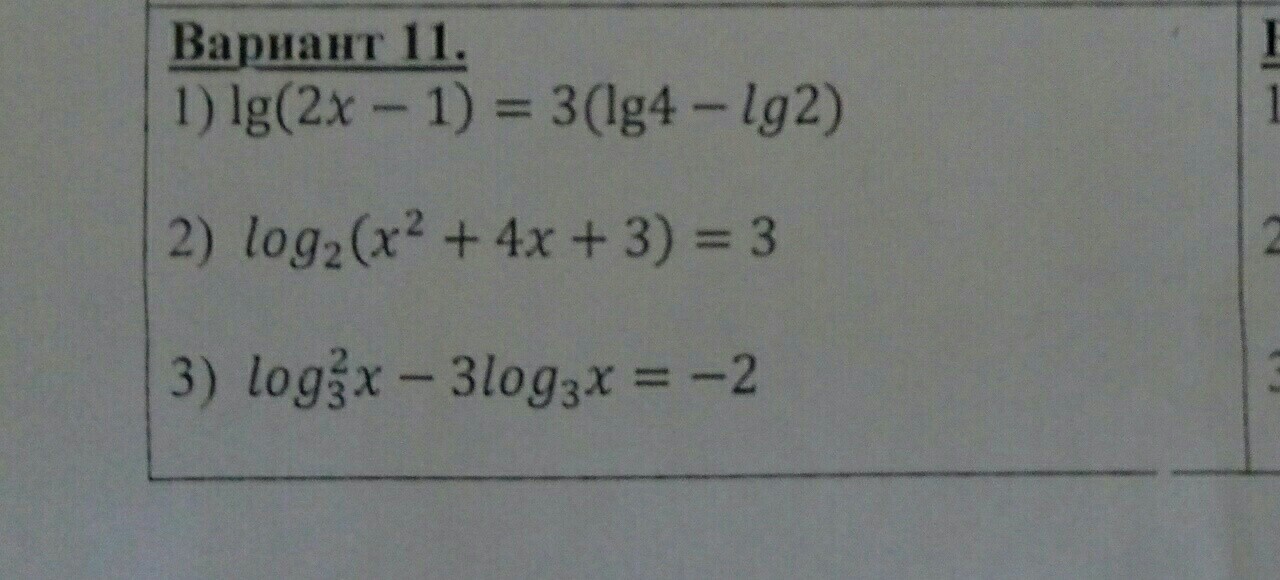
Ответы
Автор ответа:
2
ОДЗ:
Ответ:
ОДЗ: (это неравенство можно решить методом интервалов, но это "труднее", чем решить само логарифмическое уравнение; в результате нужно подставить полученный ответ в неравенство и проверить его истинность).
Подставляем полученные ответы в ОДЗ и проверяем их истинность:
(подходит)
(подходит)
Ответ:
Замена:
Обратная замена:
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Астрономия,
автор: gqnsyjd7p7
Предмет: Математика,
автор: ajtzhanovabalazhan
Предмет: Геометрия,
автор: Кастиэль21