На окружности радиуса R наудачу взяты две точки. Какова вероятность того что эти точки и центр образуют тупоугольный треугольник.
Ответы
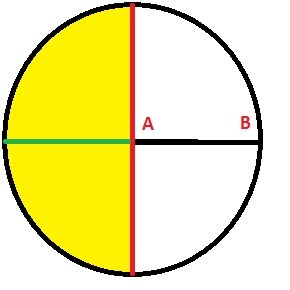
Точка А на рисунке это точка которая в центре окружности, берем вторую точку B, лежащую на три часа, если взять обычные часы за точку расчета. Или 0° если тригонометрию.
Все точки(назовем эту точки Сₓ лежащие в желтом полукруге, от 6 вечера до 12 ночи(или на языке тригонометрии 2 и 3 четверти), образуют тупой угол. Треугольник ABCₓ тупой, где бесконечное множество точек.
Тут стоит оговорится, что ровно в 6 часов и 12 часов(90° и 270° в тригонометрии) это прямоугольный треугольник, мы эти две точки не включаем. Также мы не включаем точку на 9 часов (или 180° в тр-и), т.к. это вырожденный треугольник(треугольник из одного отрезка).
Считаем точки всех тупых треугольников ABCₓ, где тупой угол A. У равнобедренного треугольника (AB=ACₓ=R) только один угол A - вершинный может быть тупым! Два боковых угла всегда острые.
A центр круга, B точка(на три часа или 0°). Точки других сторон это:
Cₓ ∈ (90°;180°) ∪ (180°;270°);
Остальные точки на окружности, которые не B равновероятны самой точке B. Поэтому вероятность ABCₓ равна вероятности всех наудачу выбранных на окружности двух точек и равна 0,4(9).
То есть почти 50%