Предмет: Алгебра,
автор: Agriee
Найти и изобразить область существования функции(подробно, если можно) 
Ответы
Автор ответа:
1
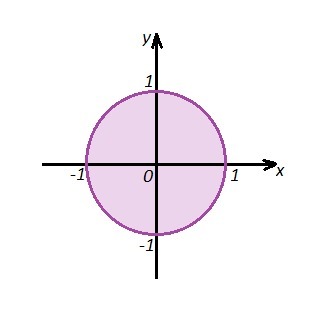
Областью определения функции будет круг с центром в начале координат и радиусом R=1 .
Приложения:
Agriee:
Неправильно функция переписана, Y не в степени, а вся скобка. По итогу получаются две параболы ( y= 1-x^2; y= -1-x^2). Понять бы только как.
1-(x^2+y)^2>=0 [формула: A^2-B^2=(A-B)(A+B) ], (1-x^2-y)*(1+x^2+y)>=0 --> y=1-x^2 , y=-1-x^2
Похожие вопросы
Предмет: Українська література,
автор: natia3999com
Предмет: Литература,
автор: More123456789
Предмет: Химия,
автор: bogancovgrigoriy
Предмет: Математика,
автор: Woostrick
Предмет: Математика,
автор: gabiknubik