Question

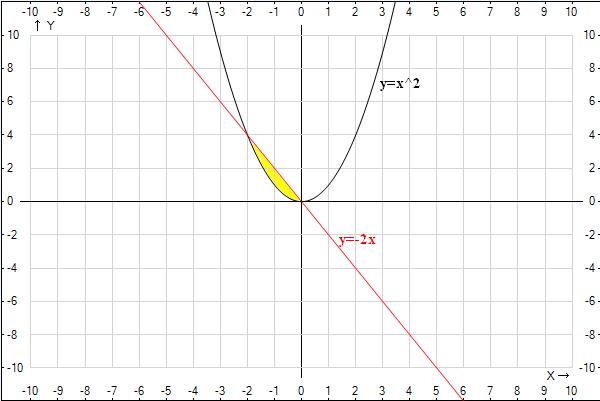
найдите площадь фигуры, ограниченной линиями 1)  y=2x^2, y=4x.       2)y=x^2, y=-2x

Answer 1

1) Для этого нужно найти интеграл разности функций:
Графики пересекаются в точках: 4x=2x^2, 2x(x-2)=0, x=0 и x=2.
$intlimits^0_2 {4x - 2x^2} , dx$ = $intlimits^0_2 {4x} , dx$ - $intlimits^0_2 {2x^2} , dx$ = (2x^2 - 2*x^3 / 3) в пределах от 0 до 2 = 2x^2*(1 - x/3) в пределах от 0 до 2 = 2*2^2*(1-2/3) - 2*0*(1 - 0/3) = 8/3 - площадь фигуры
2) аналогично первому:
графики пересекаются в точках: х=0 и х=-2
 интеграл{-2x - x^2} dx [в пределах от -2 до 0] = интеграл{-2x}dx - интеграл{x^2}dx [в пределах от -2 до 0] = -x^2 - x^3 / 3 в пределах от -2 до 0 = 4/3

Answer 2

второй пример не получилось записать через символ интеграла, криво отображал интервал

Answer 3

хорошо