Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, вычислить предел. Только распишите, пожалуйста, все подробно.
Приложения:
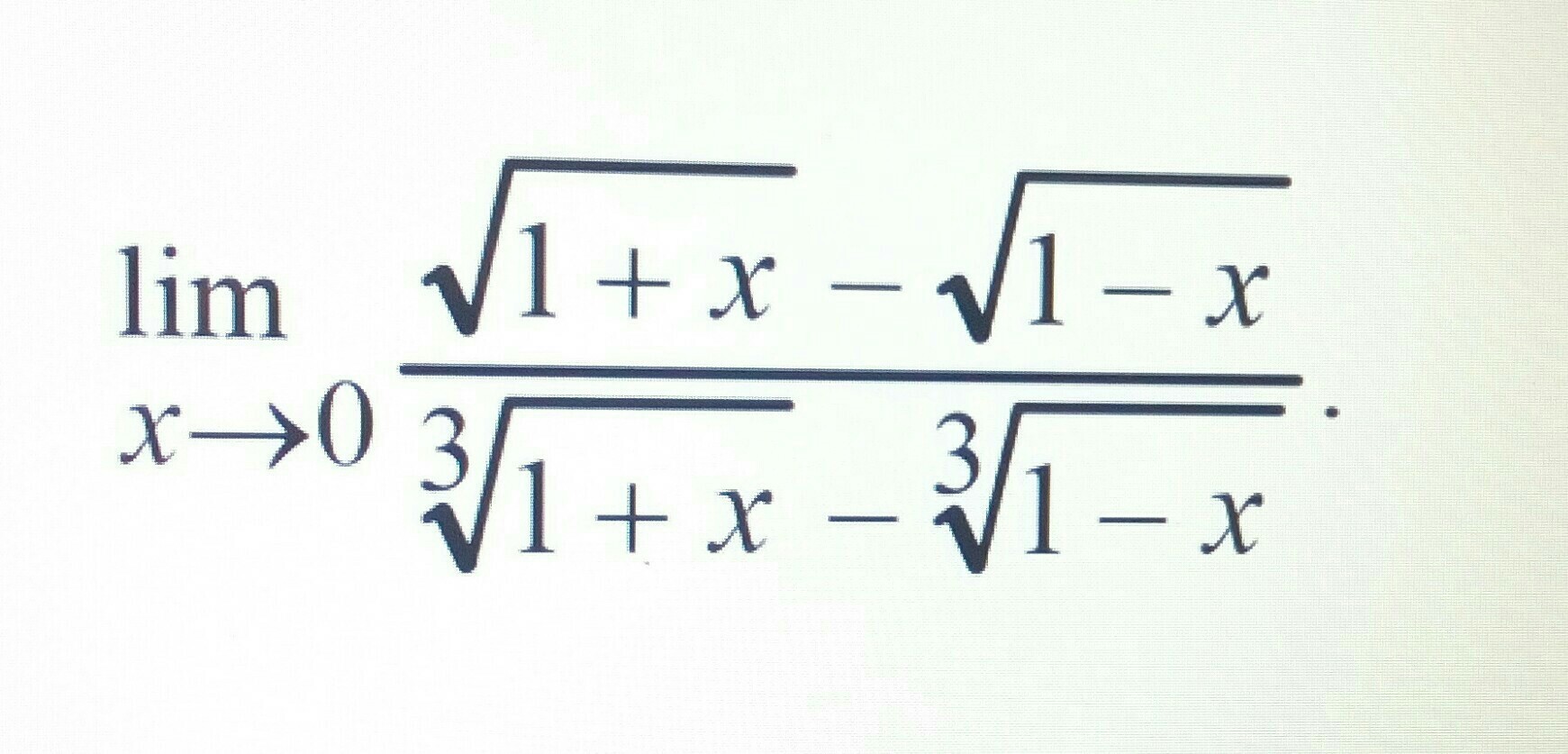
Ответы
Автор ответа:
0
NNNLLL54:
ссылку на вопрос пишите
Похожие вопросы
Предмет: Математика,
автор: rogovdv2000
Предмет: Экономика,
автор: ok191
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: Nadya600
Предмет: Математика,
автор: aigultazetdinova