Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить. Только распишите все подробно.
Приложения:
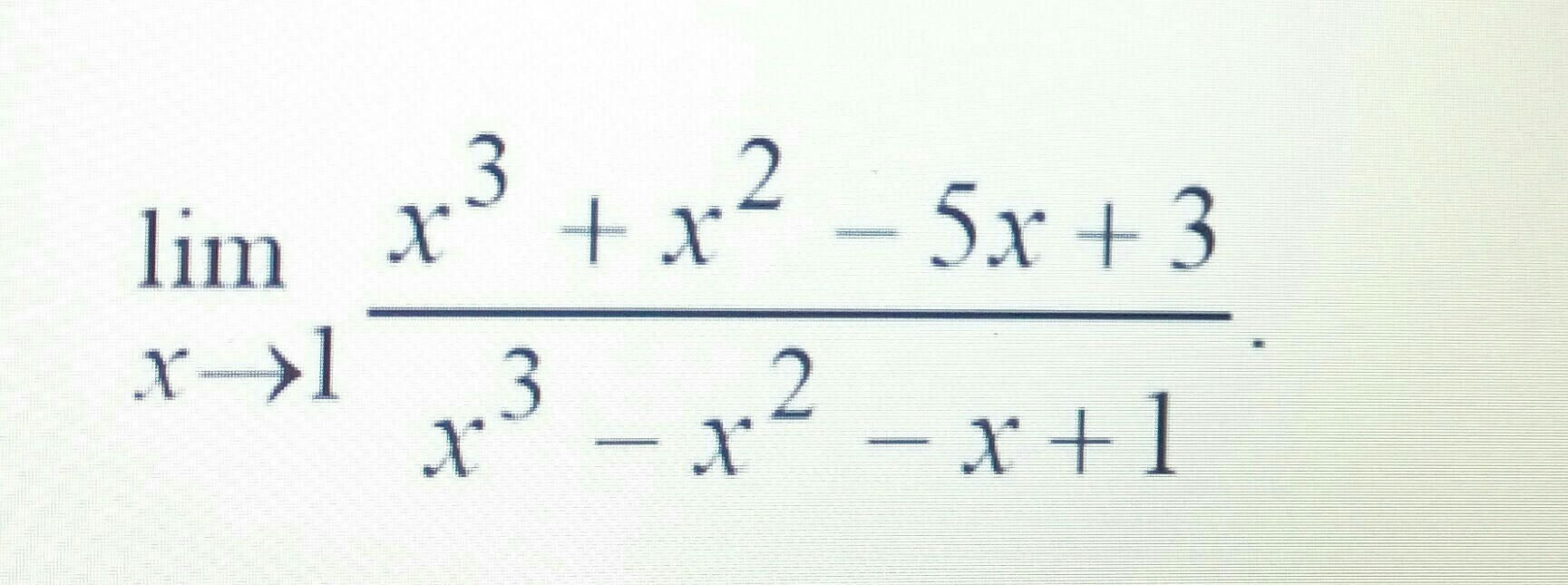
Ответы
Автор ответа:
2
Для раскрытия неопределенности разложим числитель и знаменатель на множители:
Похожие вопросы
Предмет: Окружающий мир,
автор: da0909vid
Предмет: Русский язык,
автор: joxa31d
Предмет: Қазақ тiлi,
автор: serminovansar
Предмет: Математика,
автор: travkinamasha
Предмет: Химия,
автор: lyaysenaksyano