Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, вычислить предел. Распишите, пожалуйста, все очень подробно.
Приложения:
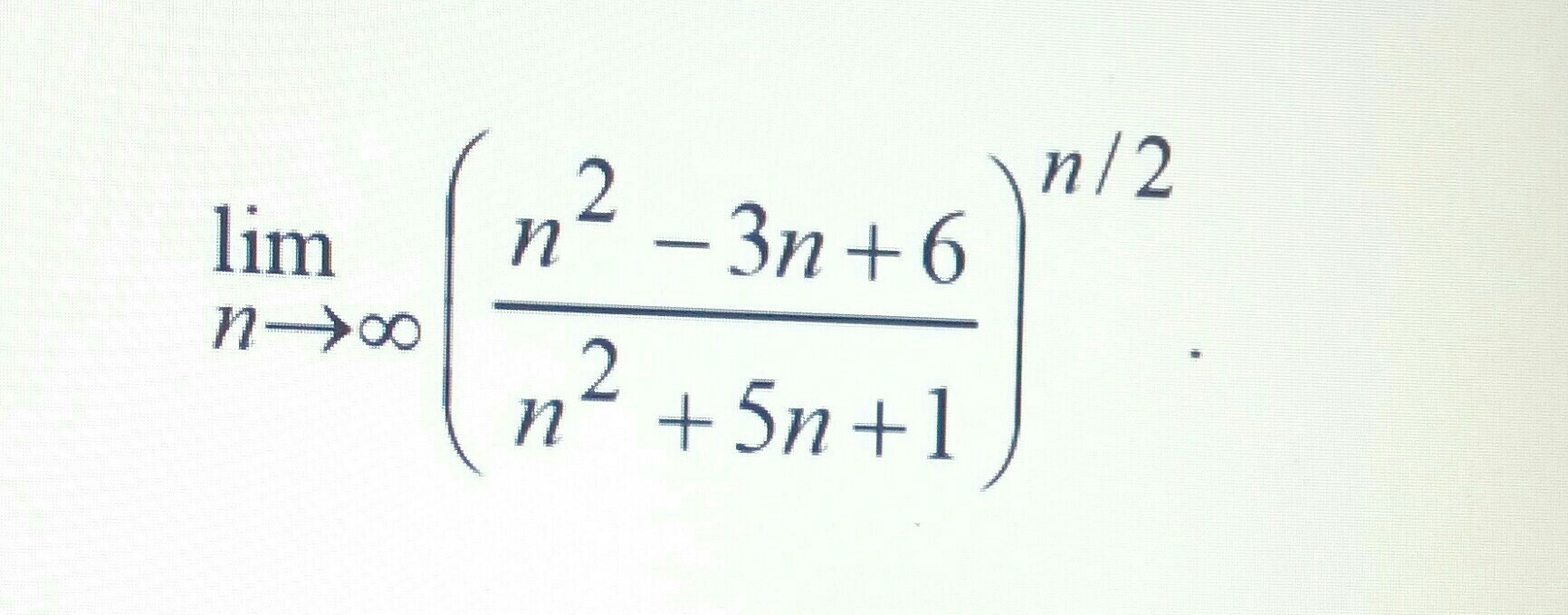
Алкадиеныч:
а что у меня не подробно?))
Ответы
Автор ответа:
6
Поскольку тут неопределённость , то нужно воспользоваться вторым замечательным пределом
Интересно, предел в скобках стремится к единице, а единица в степени бесконечность равна единице. А в ответе e^(-4).
Почему 1^(бесконечность) = 1?)
Ведь неопределённость
1∞ — это один из примеров математической неопределённости.
Там не совсем единица) Там приближенная единица. То есть может быть 0,993^беск или 1.003 в степени бесконечность. Отсюда и неопределенность)
Разделите то, что в скобках (одновременно и числитель и знаменатель на x^2). а потом подставьте бесконечность) и получится 1.
Или логарифмируя и переходить к произведению в степени. получиться что (∞ *1^{∞-1}) - по правилу лопиталя. одним из множителей второго предела является ∞, что уже говорит о том, что вычислить этот предел невозможно. Таким образом, 1^∞ является неопределённостью, и это доказано.
Я уже написал выше. ТОЧНОЙ единицы там не будет, мы будем стремится к 1 но не достигать ее. И смотря с какой стороны к 1 приближаемся отсюда и неопределенность.
Но е^(-4) приблизительно 0,0183.
так это не неопределённость а ответ)
Автор ответа:
7
Тут неопределенность бесконечность на бесконечность.
Если поделим на n^2 то получим неопределенность вида 1 в степени беск
Поработаем с тем что внутри без степени
Поделим и числитель и знаменатель на n^2
Теперь у нас неопределенность 1 в степени беск, это уже лучше, теперь тут 100% второй зам предел
Но нам же нужна единица. Так добавим и вычтем ее.
Так как мне нравится (2) вид заметельного предела, то сделаем замену на
, t стремится к 0 при n стремится к беск
Теперь нам нужно сделать такую же степень и в примере 2 зам предела
- это степень
Сосчитаем предел степени
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: masha8032008z
Предмет: Биология,
автор: yershovad
Предмет: Литература,
автор: tulengutbaevaanastas
Предмет: Математика,
автор: Svetlanka010203
Предмет: Математика,
автор: MargaritaNovikova18