Предмет: Математика,
автор: Minikoteйka
С решением, пожалуйста))
Приложения:
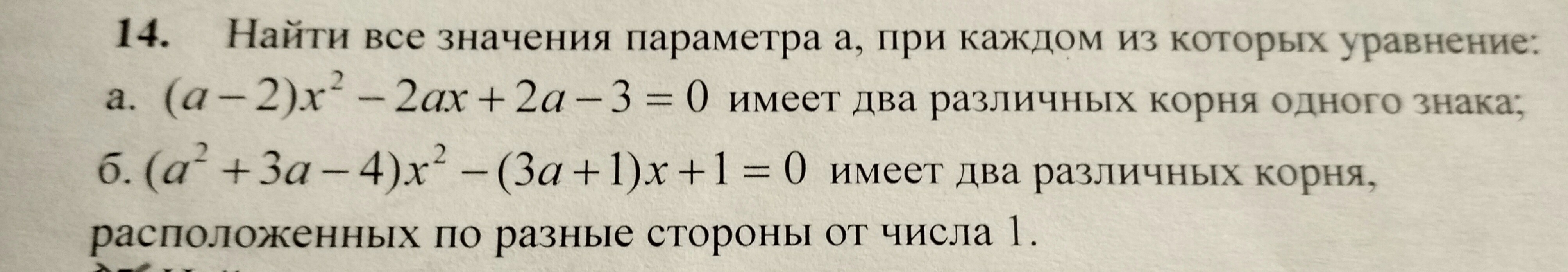
Ответы
Автор ответа:
0
а. Квадратное уравнение имеет два корня, если его дискриминант положителен. Если корни имеют одинаковый знак, то их произведение неотрицательно.
б. Рассмотрим функцию .
1. При a = -4; 1 графиком будет прямая, а она имеет с Ox не более одного пересечения. Данные значения параметра не подходят.
2. При ветви направлены вверх, тогда
3. При ветви направлены вниз, тогда
Ответ: а) б)
Похожие вопросы
Предмет: Химия,
автор: andrey47493
Предмет: Русский язык,
автор: zena508742
Предмет: География,
автор: nastiakolilol
Предмет: Алгебра,
автор: Didishka1911
Предмет: Алгебра,
автор: Alina00041