Предмет: Алгебра,
автор: klimenkol21
Найдите промежутки возрастания и убывания функции:
1) f{x)=x⁴-2x²
2) f{x)=sinx
Ответы
Автор ответа:
1
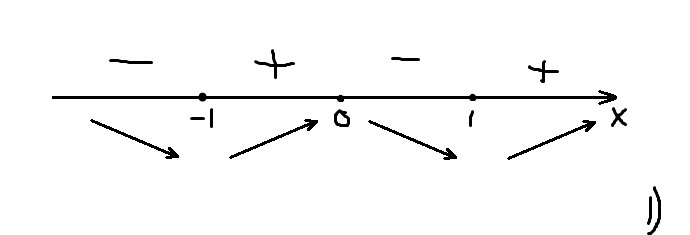
1) Найдём производную функции:
Нули производной: -1; 0; 1. , т. е. функция возрастает при
;
, т. е. функция убывает при
(см. рис. 1)
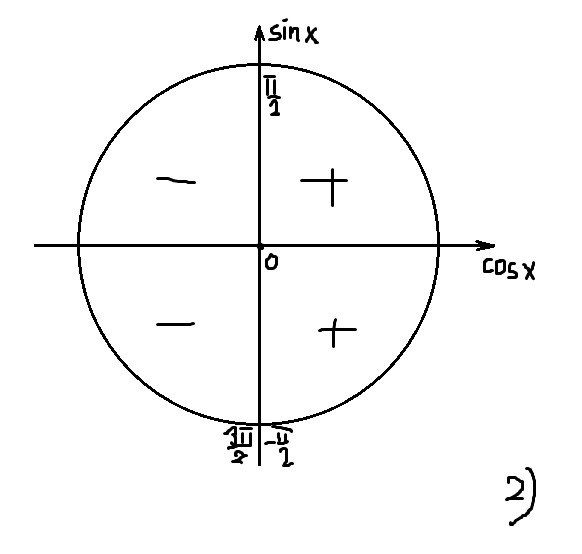
2)
Рассмотрим функцию на тригонометрической окружности (см. рис. 2). При
, т. е. функция возрастает; при
, т. е. функция убывает.
Ответ: 1) Возрастает при , убывает при
; 2) Возрастает при
, убывает при
Приложения:
Похожие вопросы
Предмет: Право,
автор: ILYAplashkov
Предмет: История,
автор: countesspanch
Предмет: Геометрия,
автор: popidans
Предмет: Математика,
автор: Milkyme