Question

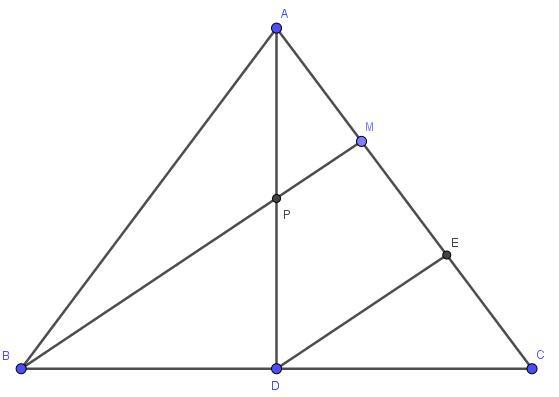
Точка P — середина высоты которая проведена к основанию BC равнобедренного треугольника ABC. Прямая BP пересекает боковую сторону AC в точке M. Докажите, что CM=2AM

Answer 1

Проведем прямую DE параллельную BM, так как AD - медиана, то

DE - средняя линия треугольника BMC, значит E - середина отрезка CM, т.е. ME = CE. Далее MP - средняя линия треугольника ADE

следовательно, AM = ME.

CM = CE + ME = ME + ME = 2ME = 2AM.

Что и требовалось доказать.