Question

У прямоугольной трапеции один из углов равен 60,прилежащая к этому углу боковая сторона равна 6 см .Найдите длину меньшего основания ,если большее основание трапеции равно 10 см

Answer 1

Опустим высоту от меньшего основания. Получим прямоугольный треугольник с углами 60 и 30 градусов и гипотенузой 6 см.

Мы знаем, что в  прямоугольном теугольнике катет лежащий против угла в 30 градусов равен половине гипотенузы. Следовательно маленький отрезок, который отсечен высотой от большого основания равен 3 см. Остальная часть основания соответственно 10-3= 7 см.

Т.к. после опускания высоты трапеция оказалась разделена на прямоугольник и треугольник, то меньшее основание тоже равно 7 см

Answer 2

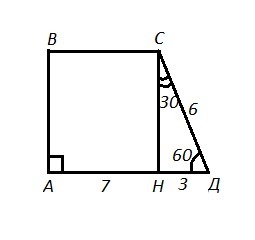
АВСД - трапеция, ∠А=∠В=90° , ∠Д=60° , СД=6 см. Найти: ВС.

Проведём СН⊥АД , получим ΔСНД, ∠СНД=90° .

∠НСД=90°-60°=30° . Против угла в 30° лежит катет НД, равный половине гипотенузы СД  ⇒  НД=1/2*СД=1/2*6=3 (см).

АД=АН+НД  ,  10=АН+3  ,  АН=10-3=7 (см).

Так как ВС║АН и АВ║СН и ∠А=∠В=90° ,  то АВСН - прямоугольник ⇒

ВС=АН=7 см