Предмет: Алгебра,
автор: Clara112
Помогите, пожалуйста, решить показательное неравенство!
Приложения:
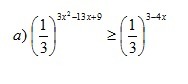
Ответы
Автор ответа:
1
Решение во вложении.
Ответ: x∈[1; 2]
Приложения:
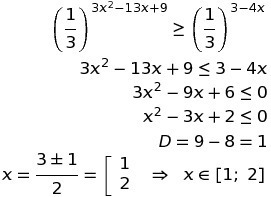
Автор ответа:
1
+ - +
---------[1]--------------[2]------------>
x ∈ [1; 2]
Похожие вопросы
Предмет: Русский язык,
автор: Kobayashii
Предмет: Английский язык,
автор: krisprofizajcev6
Предмет: Русский язык,
автор: timat2208
Предмет: Геометрия,
автор: juliaru1234