Question

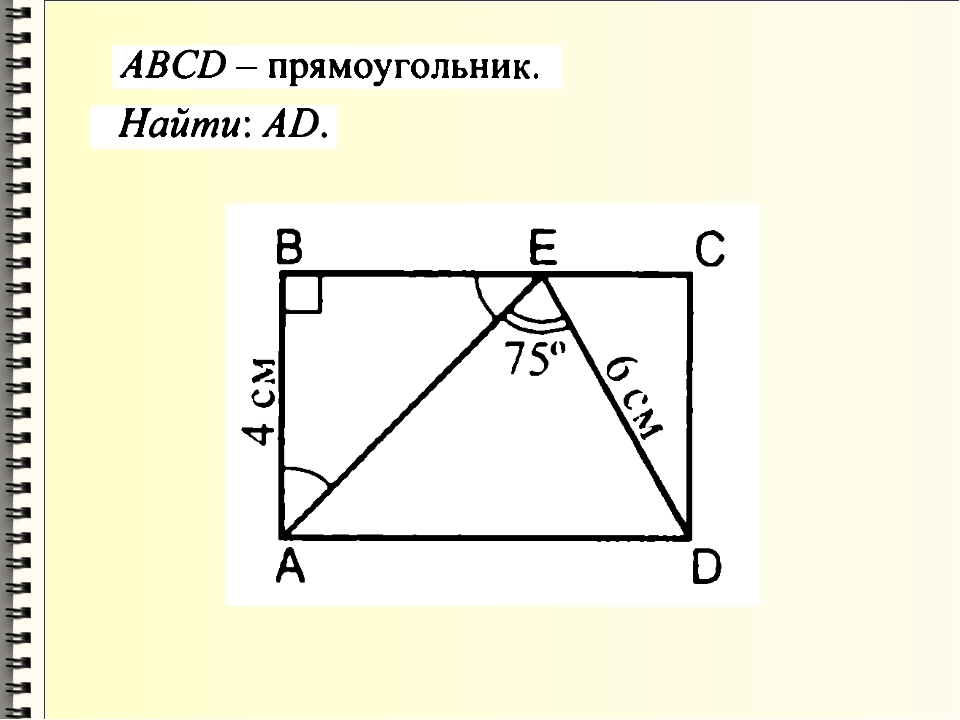
АВСД- прямоугольник, где АВ=4см, ЕД=6см. Найти длину АД. Пожалуйста помогите решить

Answer 1

Ответ:

$AD=7$ см.

Объяснение:

$\triangle ABE$ - прямоугольный и равнобедренный, значит $\angle BAE = \angle BEA = 45^{\circ}$, про свойству и $AB=BE=4$ см.

$\angle BEC = \angle BED + \angle DEC = \angle BEA + \angle AED + \angle DEC = 180^{\circ}$

$\Rightarrow \angle DEC = 180^{\circ} - \angle BEA - \angle AED = 180^{\circ} - 45^{\circ} - 75^{\circ} = 60^{\circ}$

$\triangle CED$ - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

$\Rightarrow \angle EDC = 90^{\circ} - \angle DEC = 90^{\circ} - 60^{\circ} = 30^{\circ}$.

• Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.

$\Rightarrow EC=ED:2=6:2=3$ см.

$\Rightarrow BC = BE + EC = 4 + 3 = 7$ см.

По свойству прямоугольника, $BC = AD = 7$ см.