Предмет: Алгебра,
автор: apropenred
Вычислите данное выражение.
Приложения:
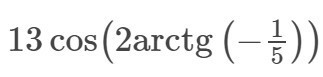
Ответы
Автор ответа:
0
Вычислить: 13cos(2arctg(-1/5))
Решение:
apropenred:
Здесь формула двойного угла?
Она самая
Похожие вопросы
Предмет: Математика,
автор: lera20092611
Предмет: История,
автор: katya941815
Предмет: Литература,
автор: miroslavklokun
Предмет: Математика,
автор: salaruman
Предмет: Физика,
автор: эльшан2