Предмет: Алгебра,
автор: Pechenka100500
Решить логарифмическое неравенство:
Приложения:
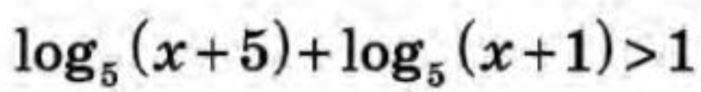
Ответы
Автор ответа:
1
ОДЗ:
С учетом ОДЗ:
Похожие вопросы
Предмет: Математика,
автор: fan441150
Предмет: Русский язык,
автор: ksyusha8273
Предмет: Русский язык,
автор: bakosofiia
Предмет: Алгебра,
автор: DariSeer