Question

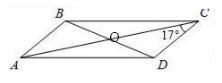
В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и ∠ACD = 17°. Най­ди­те меньший угол между диа­го­на­ля­ми параллелограмма. Ответ дайте в градусах.

Answer 1

В па­рал­ле­ло­грам­ме ABCD диа­го­наль AC в 2 раза боль­ше сто­ро­ны AB и ∠ACD = 17°. Най­ди­те меньший угол между диа­го­на­ля­ми параллелограмма. Ответ дайте в градусах.

Согласно свойствам параллелограмма его диагонали точкой пересечения делятся пополам. Имеем:

AO = OC

Так как диагональ в 2 раза больше АВ, которая в свою очередь, равна СD имеем, что половина диагонали равна им:

AO = OC = AB = CD

Рассмотрим треугольник COD:

Так как OC = СD ⇒ ΔCOD равнобедренный.

В равнобедренном треугольнике углы при основании равны:

∠COD = ∠CDO

Так как сумма внутренних углов треугольника 180° имеем:

∠CОD = (180° − ∠ACD)/2 = 163°/2 = 81,5°

Ответ: 81,5°