Предмет: Алгебра,
автор: 764Slivka
срочно. решите пожалуйста алгебру.
Приложения:
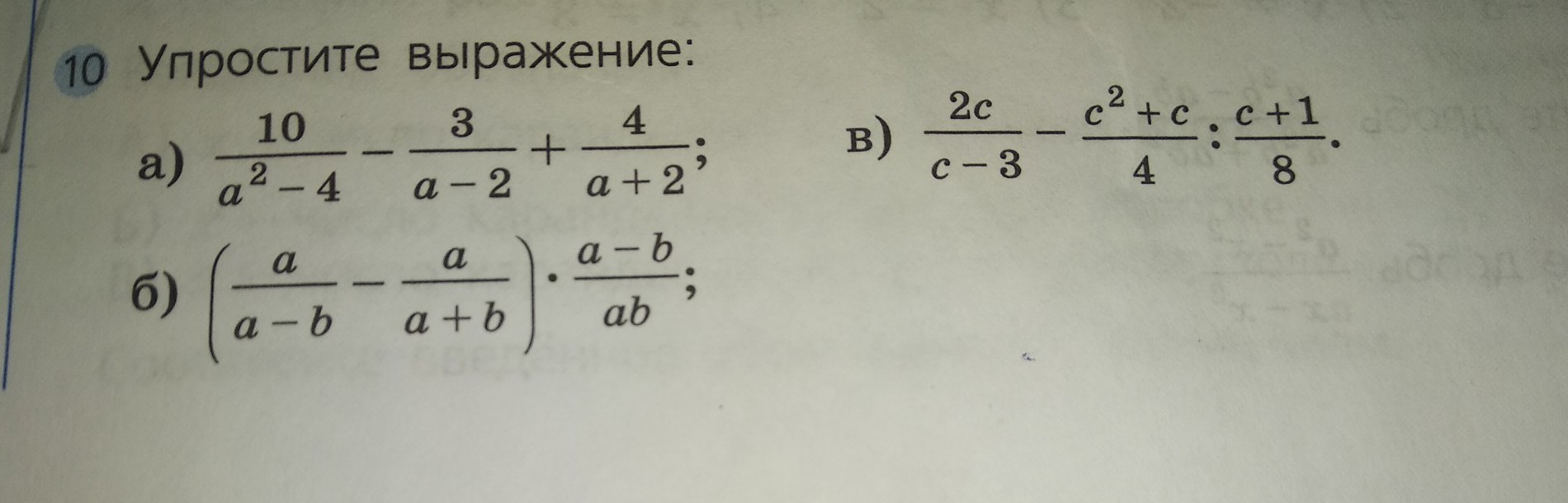
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: edditozier123
Предмет: Математика,
автор: vikakovalchyk345
Предмет: Алгебра,
автор: zelmar0507
Предмет: Математика,
автор: ahmat0001
Предмет: Математика,
автор: NameleSS184