Question

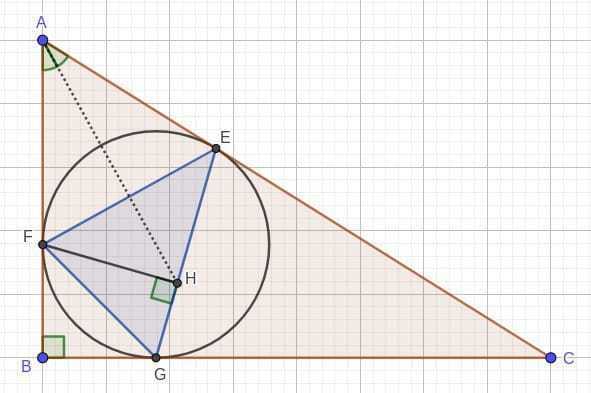
ABC - прямокутний трикутник з гіпотенузою AC. Вписане в нього коло дотикається до гіпотенузи в точці E, а до катетів AB і BC в точках F і G відповідно. FH - висота в трикутнику FEG. Доведіть, що AH - бісектриса кута BAC.

Answer 1

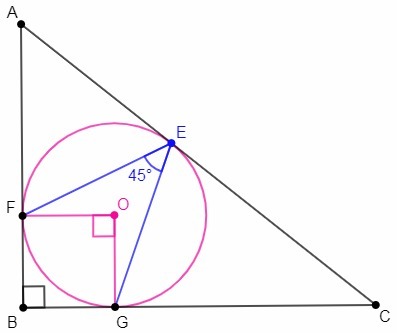
O - центр окружности

OF⊥AB, OG⊥BC (радиус, проведенный в точку касания, перпендикулярен касательной)

∠B=90 => ∠FOG=90 (сумма углов четырехугольника 360)

∠FEG=∠FOG/2=45 (вписанный угол равен половине центрального, опирающегося на ту же дугу)

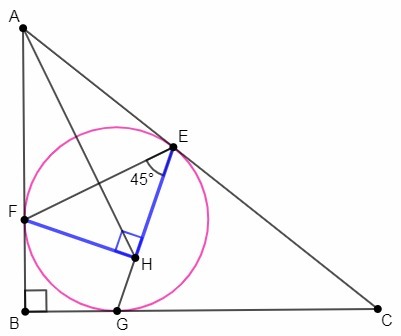
△FHE - равнобедренный (прямоугольный с углом 45), FH=EH

AF=AE (отрезки касательных, проведенных из одной точки)

△AFH=△AEH (по трем сторонам), ∠FAH=∠EAH, AH - биссектриса