Предмет: Геометрия,
автор: gzm7c
В угол вписана окружность з радиусом R. Длина хорды, которая соединяет точки касания, равна а. К окружности проведены две касательные, параллельные к хорде. Найти площадь полученной трапеции.
P.S. Учитель сказал, что решать нужно через подобие треугольников
Ответы
Автор ответа:
2
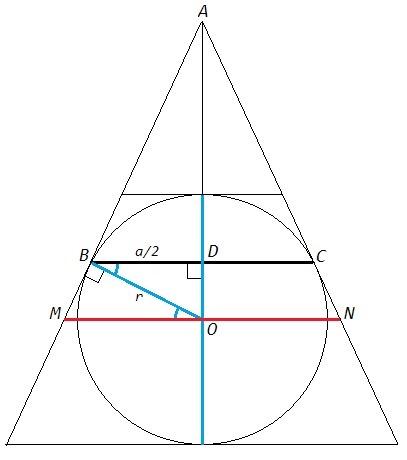
MN - средняя линия трапеции. Средняя линия проходит через центр вписанной окружности.
Отрезки касательных из одной точки равны, △BAC - равнобедренный. Параллельные линии отсекают от угла подобные треугольники. Средняя линия MN параллельна основаниям, основания параллельны BC, MN||BC => △MAN~△BAC, △MAN - равнобедренный. Центр вписанной окружности лежит на биссектрисе. Биссектриса в равнобедренном треугольнике является высотой и медианой, ∠BDO=90, BD=BC/2=a/2, MO=MN/2.
Радиус перпендикулярен касательной, ∠OBM=90.
Накрест лежащие углы при параллельных равны, ∠MOB=∠OBD.
△MOB~△OBD (по двум углам)
MO/OB=OB/BD <=> (MN/2)/r=r/(a/2) <=> MN=4r^2/a
В трапецию вписана окружность, h=2r.
S=MN*h =4r^2/a *2r =8r^3/a
Приложения:
Похожие вопросы
Предмет: История,
автор: saryjegor00
Предмет: Физика,
автор: fadeevaaleks25
Предмет: Алгебра,
автор: kirillaleynikov
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: msmilenaa