Предмет: Алгебра,
автор: smirnovar2016
Пожалуйста мне очень нужна ваша помощь,срочно нужно решение,всё на картинке
Приложения:
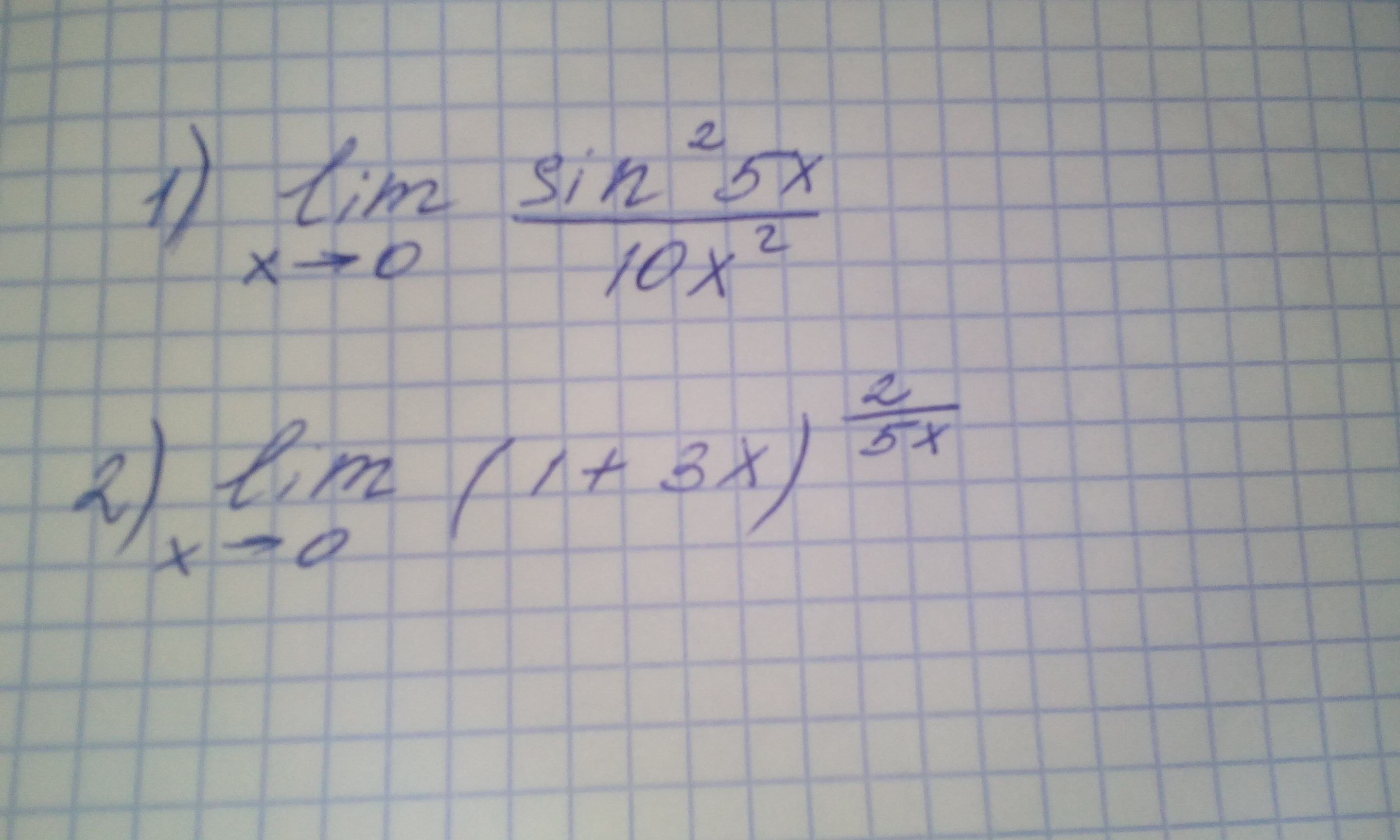
Ответы
Автор ответа:
1
smirnovar2016:
Спасибо вам огромное!!!
Похожие вопросы
Предмет: Алгебра,
автор: kaztarik63
Предмет: Алгебра,
автор: ventisas11
Предмет: Українська мова,
автор: estudiante23
Предмет: Биология,
автор: julyap
Предмет: Обществознание,
автор: ansa1