Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, вычислить предел. Подробно.
Приложения:
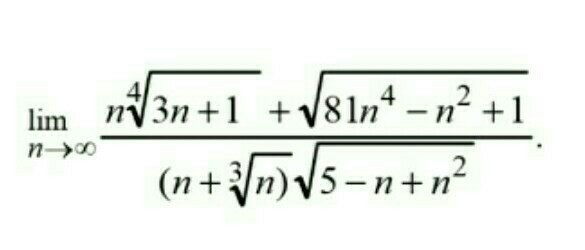
Ответы
Автор ответа:
2
maksimcat:
81-1/n^2+1/n^2 (1/ n^2 или 1/n^4 ?)
+1/n^4
Ок
Похожие вопросы
Предмет: Геометрия,
автор: anastasiafisic
Предмет: Биология,
автор: DimonchikLimonchik3
Предмет: История,
автор: tasmasysanastasi
Предмет: Математика,
автор: begonia
Предмет: Алгебра,
автор: murmurblya