Предмет: Алгебра,
автор: daniil0723
Решите логарифмическое уравнение
Приложения:
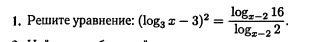
oganesbagoyan:
x -2 > 0 и x-2 ≠ 1 || x > 2 и x ≠ 3 || * * * x∈ (2 ; 3) ∪ (3 ;∞) * * *
Ответы
Автор ответа:
1
(log₃ x - 3)²=
(log₃ x - 3)²=log₂16, x>3, x ≠ 2; соответственно x ≠ 2 cоблюдается из неравенства x>3
(log₃ x - 3)²=4
(log₃ x - 3)²-4=0
(log₃x -3-2)(log₃x-3+2)=0
(log₃x - 5)(log₃x -1)=0
log₃ x - 5 =0
log₃x=5
log₃x=5log₃3
log₃x=log₃3⁵
x=3⁵
log₃x-1=0
log₃x=1
log₃x=log₃3
x=3 - не входит в одз.
Ответ х = 3⁵
Сверху я просто переписал пример, на символы не обращай внимания
Вторая строка x >2 ; x ≠ 3
Да-да, совсем забыл!
исправьте, время позволяет
исправьте x >2 ; x ≠ 3 * * * если x >3 , то автом. x ≠ 2 * * *
Автор ответа:
0
task/30049594 решите уравнение (log₃ ˣ -3)² = logₓ₋₂ 16 / logₓ₋₂ 2
решение ОДЗ: { x >0 ; x-2>0; x -2 ≠1.⇒{ x >2 ; x ≠3. т.е. x∈(2 ; 3) ∪ (3 ;∞)
logₓ₋₂ 16 / logₓ₋₂ 2 = logₓ₋₂ 2⁴ / logₓ₋₂ 2 =4logₓ₋₂ 2 / logₓ₋₂ 2 =4
(log₃ ˣ - 3)² = 4 ⇔ (log₃ ˣ -3)² - 2² =0 ⇔ (log₃ ˣ -3 -2)(log₃ ˣ -3 +2) =0⇔
(log₃ ˣ - 5)(log₃ ˣ -1) =0 ⇔[ log₃ ˣ - 5 = 0 ;log₃ ˣ -1 =0. ⇔ [ log₃ ˣ =5; log₃ ˣ= 1.⇔
[ x=3⁵ ; x=3 ∉ ОДЗ (посторонний корень ). x=3⁵=243
ответ : 243 .
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: zvdaalea
Предмет: История,
автор: yaroslavpolischuk11
Предмет: Биология,
автор: Веруня17