Предмет: Математика,
автор: o2142582
Найти производную функции, можно пожалуйста подобно.
Приложения:
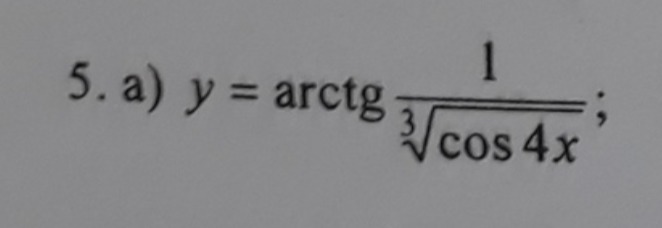
Ответы
Автор ответа:
1
Если это матан универский, а скорей всего это он и есть) то получается такая штука.
Приложения:


o2142582:
да, но откуда эти степени ?
Упс. Прошу прощения) первого минуса нету...
Попробую Вам на пальцах объяснить. Сейчас перепишу решение
мне просто не понятен именно момент с -4/3 степенью. Не могли бы вы пояснить ?
я понимаю, почему -1/3 , но откуда -4/3 понять не в состоянии.
Я добавил фотку. Попробуйте разобраться.
Не забудьте только убрать минус перед первой дробью. А вообще чувак снизу заморочился и привел в более красивоому виду, у него тоже правильно)
Автор ответа:
0
Докажем, что
Дадим к приращение
, тогда
и
получат приращения
и
соответственно. Пусть при
.
Тогда, имеет место .
Переходя к пределам при , получим:
или, что эквивалентно: .
По индукции можно доказать что .
Тогда, исходя из доказанного утверждения, найдём производную:
Похожие вопросы
Предмет: Русский язык,
автор: Maksim228456
Предмет: Биология,
автор: darakudrakova2
Предмет: Обществознание,
автор: Chazokov
Предмет: Математика,
автор: Аноним