Предмет: Алгебра,
автор: Margo427
прошу помогите !!!Очень надо
даю 20 баллов
Приложения:
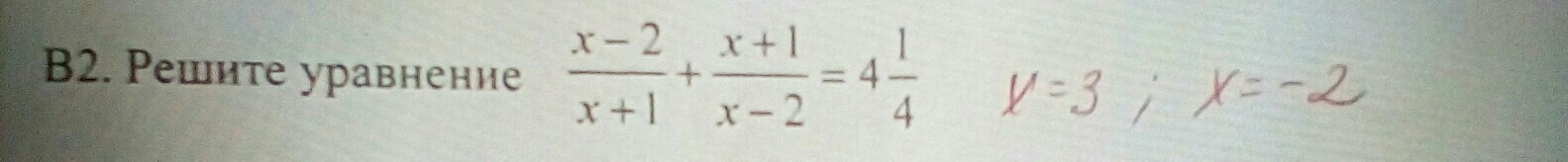
Ответы
Автор ответа:
1
х ≠ -1, х ≠ 2
Решаем с помощью дискриминанта:
Находим t:
Подставляем:
↓
Ответ: х1 = -2, х2 = 3
Похожие вопросы
Предмет: Русский язык,
автор: sonya2590
Предмет: Английский язык,
автор: darynkaproshyn
Предмет: Музыка,
автор: mishleinsima
Предмет: Алгебра,
автор: pro100Steg