Предмет: Алгебра,
автор: arinabazikova
Доказазать неравенство
Приложения:
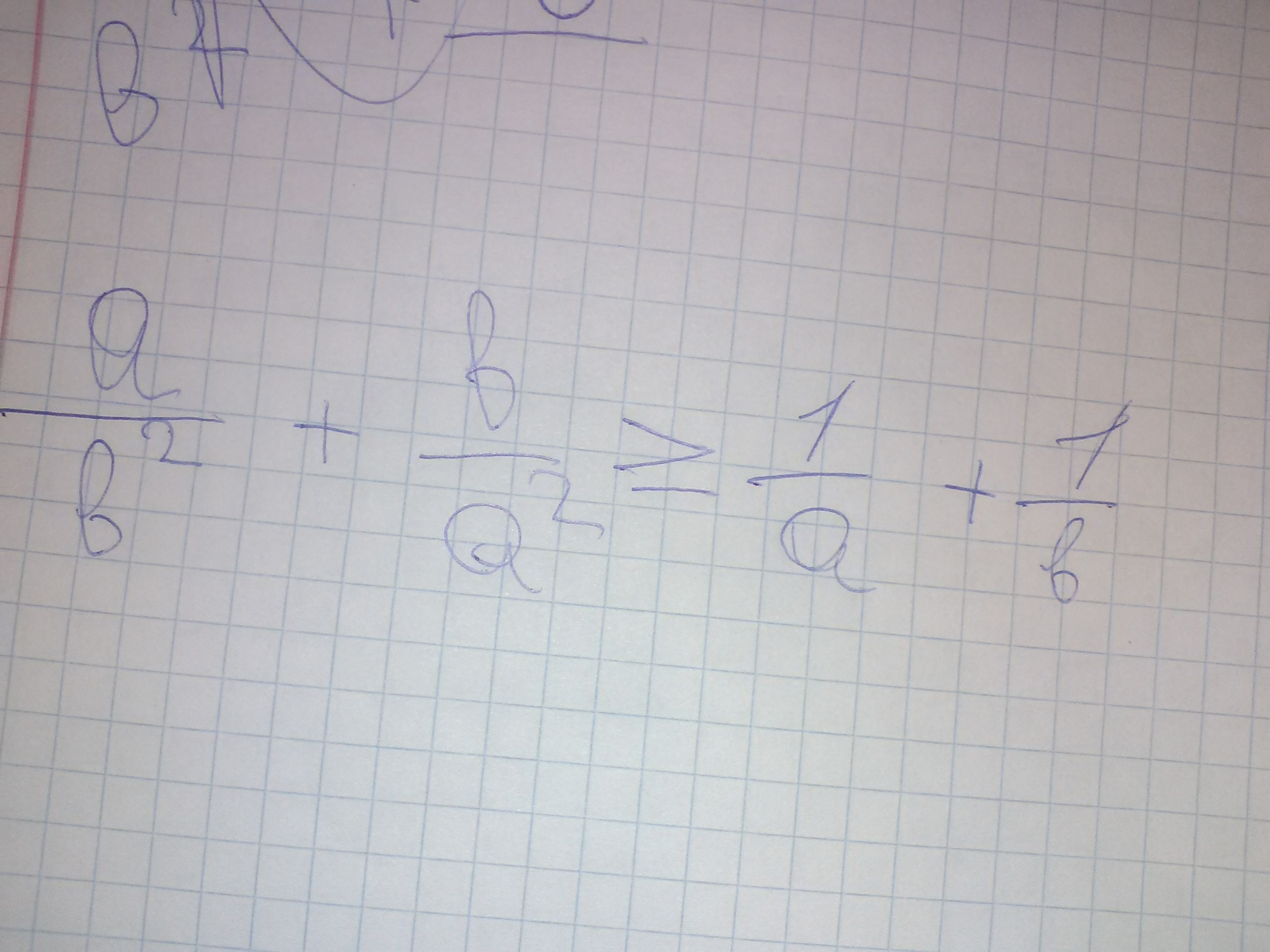
Ответы
Автор ответа:
0
Утверждение, которое мы получили равносильно данному. При:
оно верно, т. к. квадраты чисел неотрицательны, ч. т. д.
Похожие вопросы
Предмет: Литература,
автор: onegine58
Предмет: Алгебра,
автор: bezruchko2023
Предмет: Алгебра,
автор: lolll28
Предмет: Алгебра,
автор: ellabcgbvc
Предмет: Физика,
автор: darenka1