Предмет: Алгебра,
автор: Pechenka100500
Решить логарифмические неравенства:
Приложения:
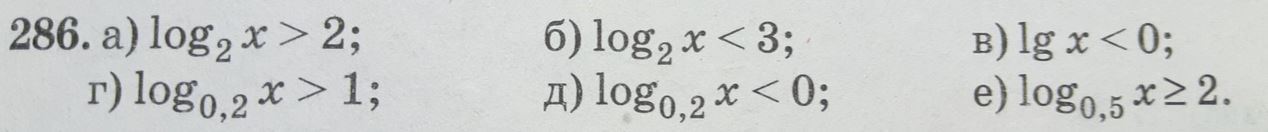
Ответы
Автор ответа:
0
Логарифмическая функция при основании > 1 явл. возоастающей, и знак неравенства между аргументами не изменяется. А если основание логарифмической функции < 1 , то знак неравенства изменяется на противоположный при сравнении аргументов.
NNNLLL54:
Да, подкорректировала
Автор ответа:
0
Похожие вопросы
Предмет: Музыка,
автор: mhm235
Предмет: Английский язык,
автор: vkxhfhvhhuc
Предмет: Музыка,
автор: nataslbd
Предмет: Геометрия,
автор: ОляМитяева
Предмет: История,
автор: Зилола11