Предмет: Алгебра,
автор: NonameI
Помогите решить уравнение
Приложения:
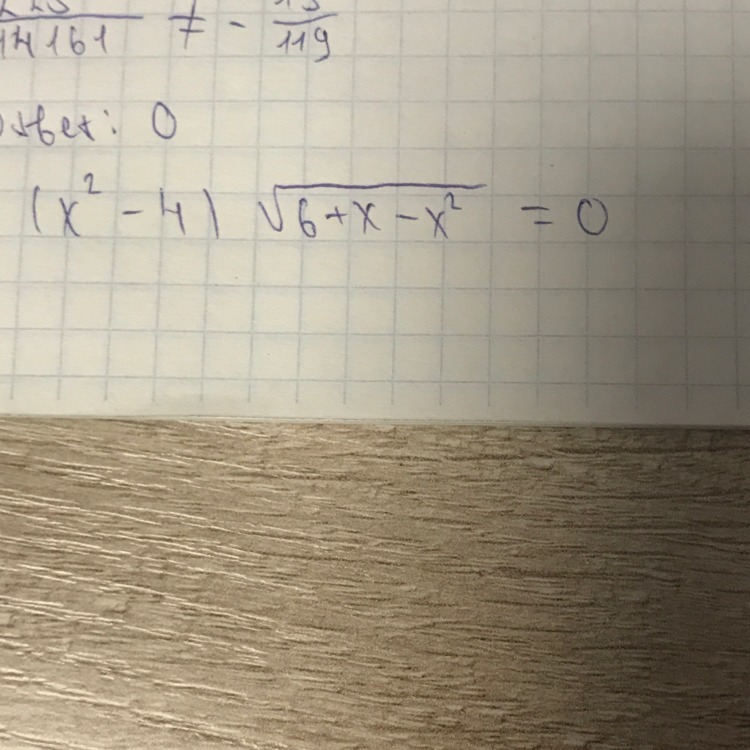
Ответы
Автор ответа:
0
ОДЗ: 6+x-x²≥0
D=1+4*6=5²;
x1=(-1+5)/-2=-2;
x1=(-1-5)/-2=3;
- + -
_____-2_______3_______
-2≤x≤3
если множители дают ноль, то сами множители равны нулю^
6+x-x²=0
это мы уже решили выше.
x²-4=0;
x=-2;
x=2;
x1=-2; x2=2; x3=3;
Автор ответа:
9
Ответ: х1 = -2, х2 = 2, х3 = 3
yehnxgx:
помогите мне пожалуйста с алгеброй вопрос в профиле
Похожие вопросы
Предмет: Математика,
автор: dhejdjhfgjybjrkfjf
Предмет: Английский язык,
автор: asemkumenova
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: nburkaeva