Предмет: Геометрия,
автор: ovs75rus
Даю 50 баллов. длины двух сторон треугольника равны 15 и 12 см. Они образуют острый угол, синус которого равен 4/5, Найдите квадрат медианы, проведенной к третьей стороне.
Ответы
Автор ответа:
1
АМ²=?
найдем третью сторону AC
по теореме косинусов

(так как а - острый угол, то

)
по т Стюарта квадрат медианы


найдем третью сторону AC
по теореме косинусов
(так как а - острый угол, то
)
по т Стюарта квадрат медианы
Приложения:
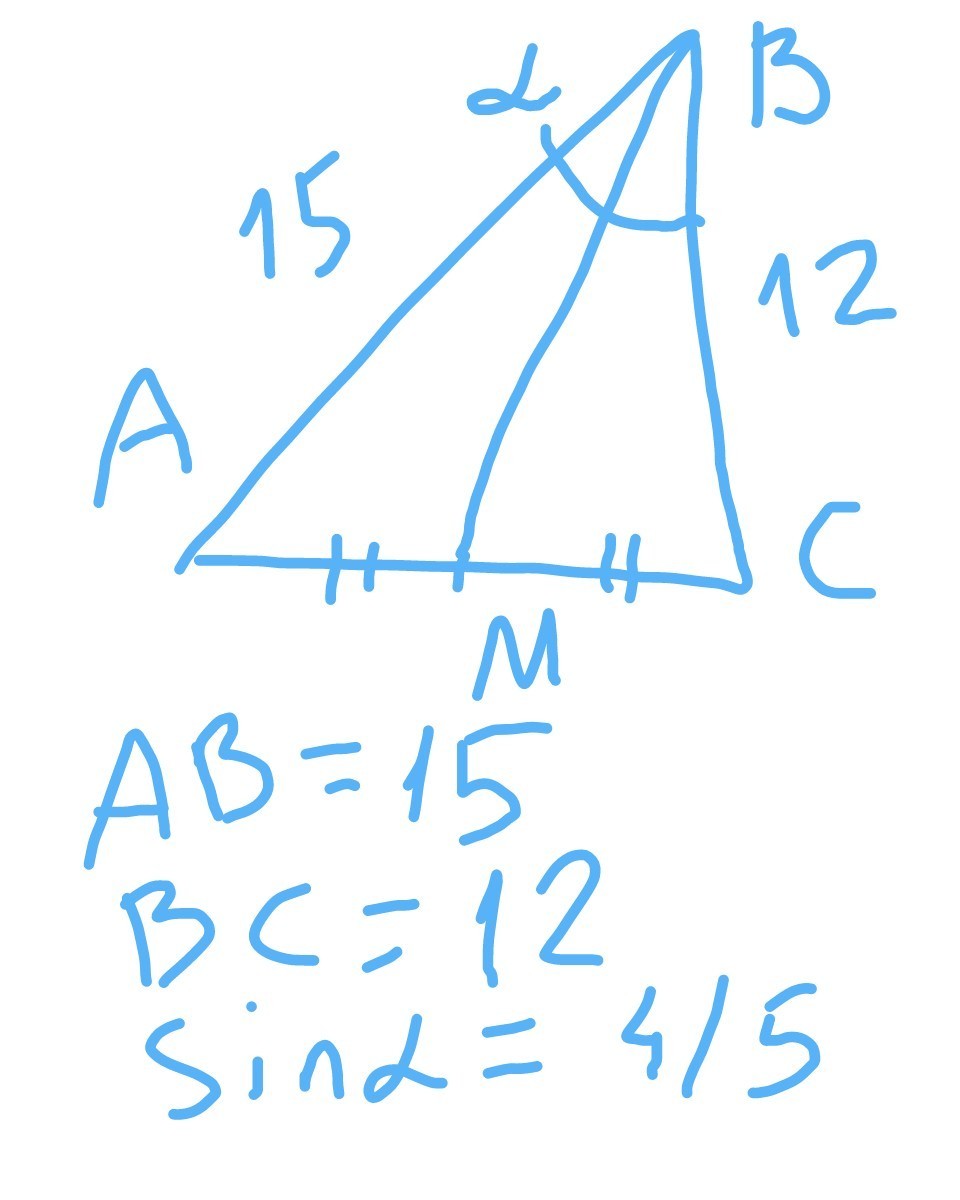
Похожие вопросы
Предмет: Биология,
автор: shimmershimmer2007
Предмет: Қазақ тiлi,
автор: indiramarsova1
Предмет: История,
автор: SERGO7227
Предмет: Математика,
автор: дима1066
Предмет: Математика,
автор: Екатерина1111885