Question

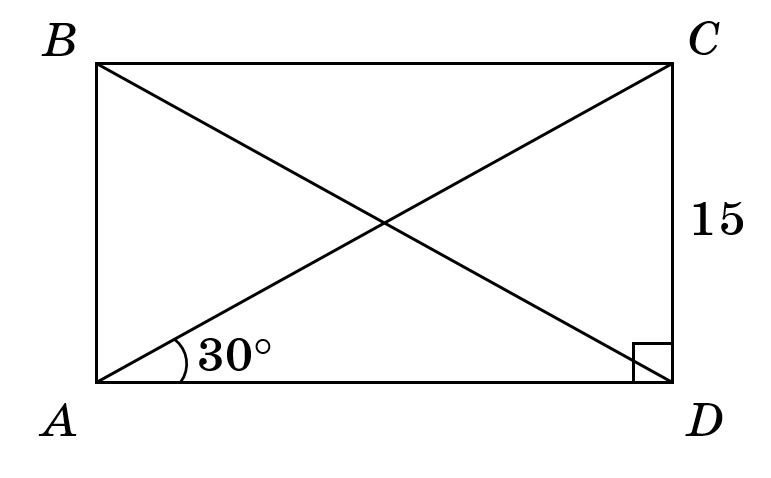
Найти диагонали прямоугольника ABCD,если < CAD=30 градусам ,CD=15 см.
СРОЧНО!

Answer 1

Дано: $ABCD$ — прямоугольник ⇒ $AB = CD = 15$ см, $BC = AD$; $\angle CAD = 30^{\circ}$.

Найти: $AC - ? \ BD - ?$

Решение. По свойству прямоугольника его диагонали равны: $AC = BD.$ Одна его диагональ делит прямоугольник на два равных прямоугольных треугольника.

Рассмотрим $\triangle ADC (\angle ADC = 90^{\circ}):$

$\text{sin}\angle CAD = \dfrac{CD}{AC} \Rightarrow AC = \dfrac{CD}{\text{sin}\angle CAD} = \dfrac{15}{\text{sin}30^{\circ}} = \dfrac{15}{\dfrac{1}{2}} = 30$ см.

Ответ: $AC = BD = 30$ см.