Предмет: Математика,
автор: fmamedova48
189-199 пожалуйста с объяснением
Приложения:

Ответы
Автор ответа:
1
189. если под корнем находятся числа с той же степенью то они выносятся из под знака корня без степени /то же самое что возвести в квадрат и вынести из под знака корня/ далее элементарное решение.

190. это то же самое что и 189.

191. Здесь мы выносим общий множитель за скобку и прибавляем числа. дальше мы просто находим корни этих чисел /49=7*7, 1,69=1,3*1,3/

192. здесь так же как и в 191.

193. и 194. если честно, не знаю... чуть позже напишу
195. при х=10, у=-6 (похоже на 189 и 190) /четная степень всегда дает положительное число/

196. почти так же как и 195. а= 12, в=-5

197.

190. это то же самое что и 189.
191. Здесь мы выносим общий множитель за скобку и прибавляем числа. дальше мы просто находим корни этих чисел /49=7*7, 1,69=1,3*1,3/
192. здесь так же как и в 191.
193. и 194. если честно, не знаю... чуть позже напишу
195. при х=10, у=-6 (похоже на 189 и 190) /четная степень всегда дает положительное число/
196. почти так же как и 195. а= 12, в=-5
197.
parus77:
189,190,195 надо делать так же как и 196.
Автор ответа:
1
применяем св-ва действия с квадратным корнем(смотри в учебнике),а решение примеров(кроме 193 и 194-не помню как их вычислять) смотри внизу.
Приложения:
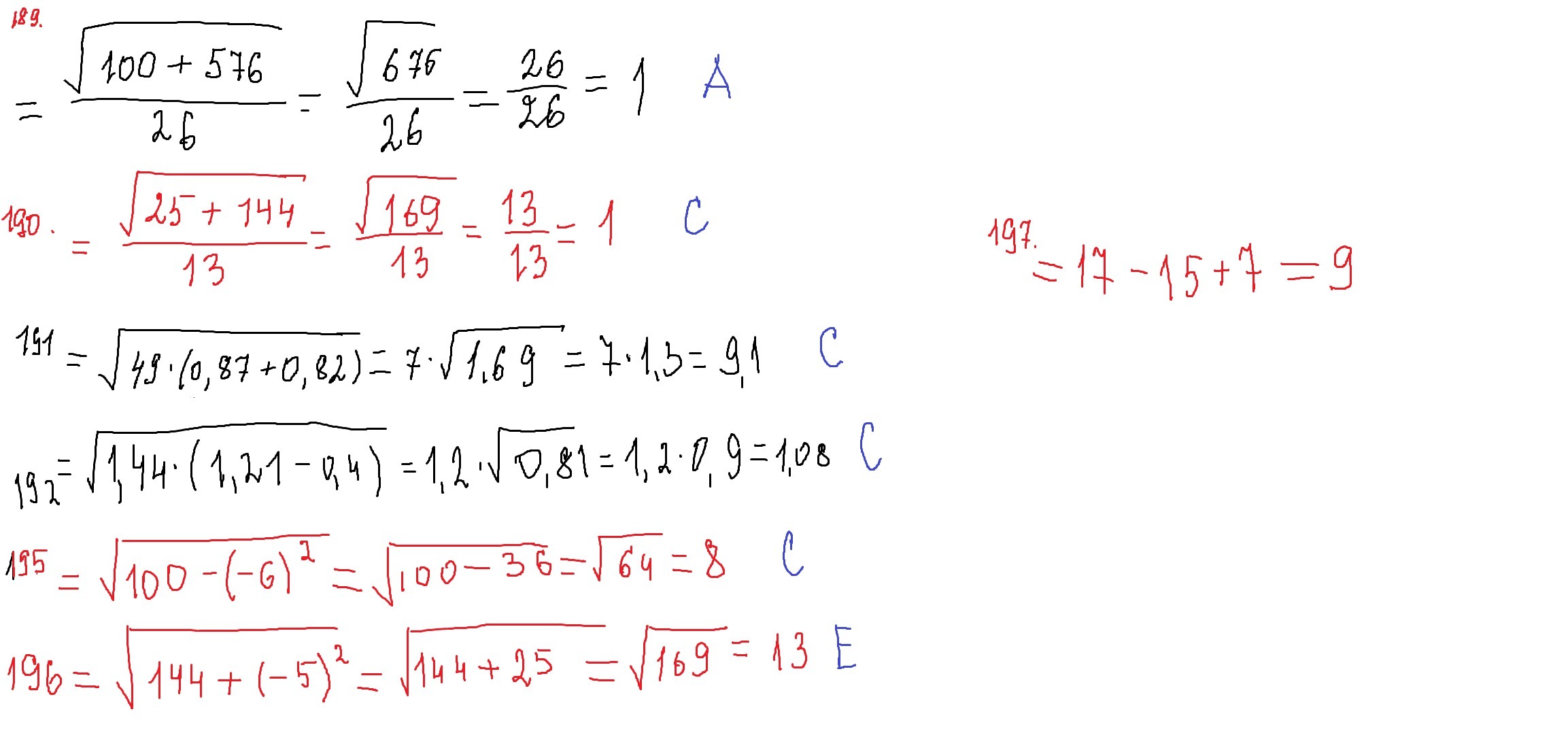
Похожие вопросы
Предмет: Математика,
автор: dashylka1517
Предмет: Геометрия,
автор: katyha1329
Предмет: Литература,
автор: altairayas5
Предмет: Алгебра,
автор: алина45657