Предмет: Математика,
автор: PandERS01xbet
Помогите решить пример
Найдите значение дроби
Приложения:
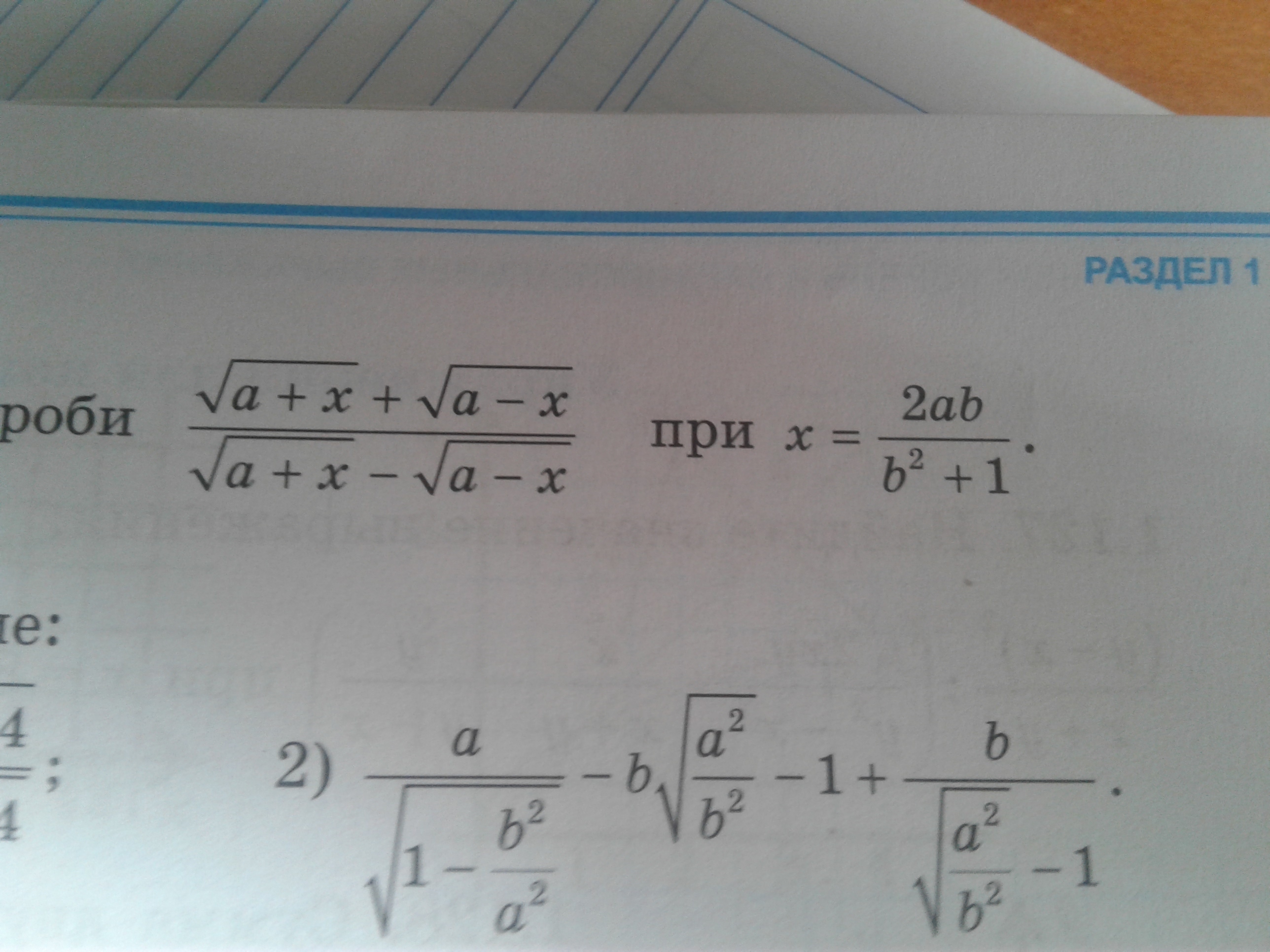
Ответы
Автор ответа:
1
если , то
PandERS01xbet:
Спс
Похожие вопросы
Предмет: География,
автор: sabina040309
Предмет: Информатика,
автор: xeniashamuratova
Предмет: Русский язык,
автор: demfud
Предмет: Химия,
автор: pspsps55
Предмет: Физика,
автор: IngaNovikova