Question

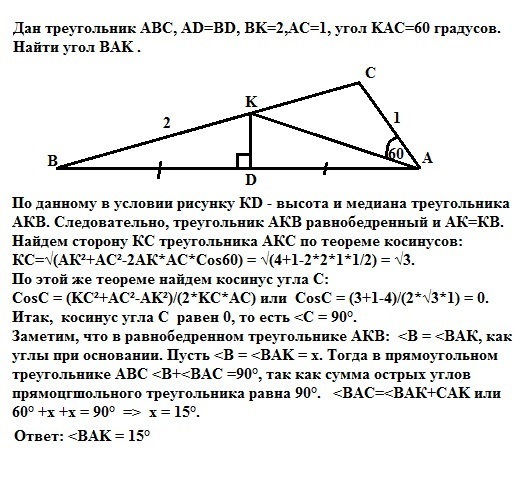
Дан треугольник ABC, AD=BD, BK=2,AC=1, угол KAC=60 градусов, найти угол BAK

Answer 1

По данному в условии рисунку КD - высота и медиана треугольника АКВ. Следовательно, треугольник АКВ равнобедренный и АК=КВ. Найдем сторону КС треугольника АКС по теореме косинусов: КС=√(АК²+АС²-2АК*АС*Cos60) = √(4+1-2*2*1*1/2) = √3.

По этой же теореме найдем косинус угла С:

CosC = (KC²+AC²-AK²)/(2*KC*AC) или  CosC = (3+1-4)/(2*√3*1) = 0. Итак,  косинус угла С  равен 0, то есть <C = 90°.

Заметим, что в равнобедренном треугольнике АКВ:  <B = <ВАК, как углы при основании. Пусть <B = <BAK = x. Тогда в прямоугольном треугольнике АВС <B+<BAC =90°, так как сумма острых углов прямоцгшольного треугольника равна 90°.   <BAC=<ВAК+CAK или 60° +х +х = 90°  =>  x = 15°.

Ответ: <BAK = 15°