Предмет: Алгебра,
автор: lilroxy2k
Помоги пожалуйста!
Срочно.
Доказать, что выражение не зависит от переменной.
Приложения:
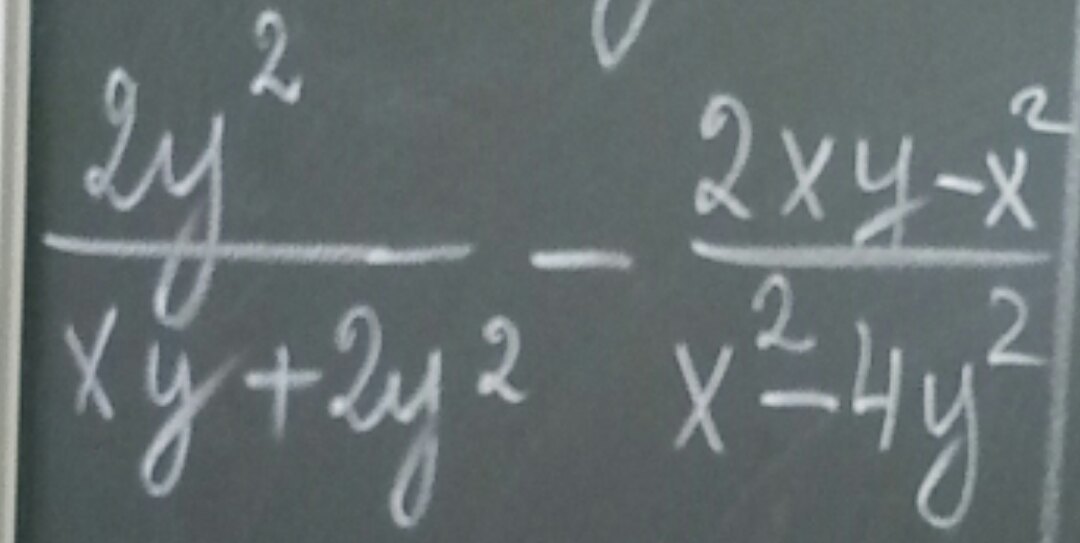
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Беларуская мова,
автор: nastakozun
Предмет: Математика,
автор: 79wu
Предмет: Геометрия,
автор: Аноним
Предмет: Алгебра,
автор: vika6416265
Предмет: Геометрия,
автор: martinabela