Предмет: Математика,
автор: egri
разложить многочлен (2(t^2)+3)/((t^3)+3t) ответ я знаю, но я не могу расписать как он получен, нужно как то методом неопределенных коофецентов я пологаю
Приложения:
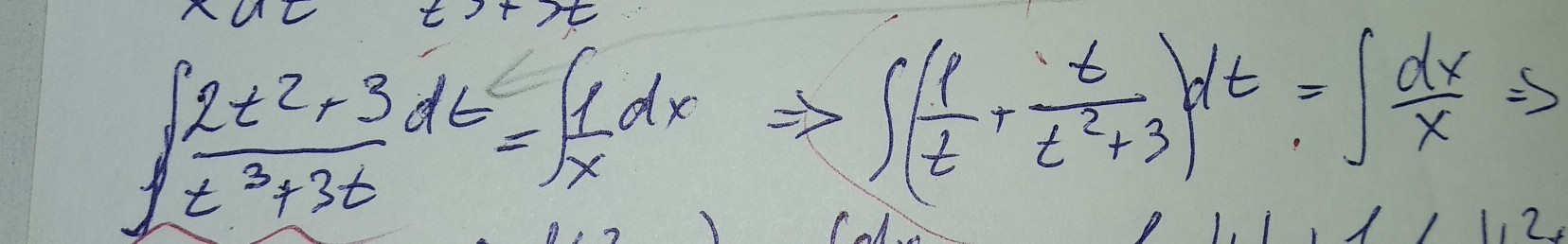
Ответы
Автор ответа:
1
приравнивается равные коэффициенты при одинаковых степенях t
поэтому
Похожие вопросы
Предмет: История,
автор: shkolnikvonyayet
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: burndie34
Предмет: Физика,
автор: LENAVOLK11
Предмет: Алгебра,
автор: sia87