Предмет: Геометрия,
автор: sirrhaegar
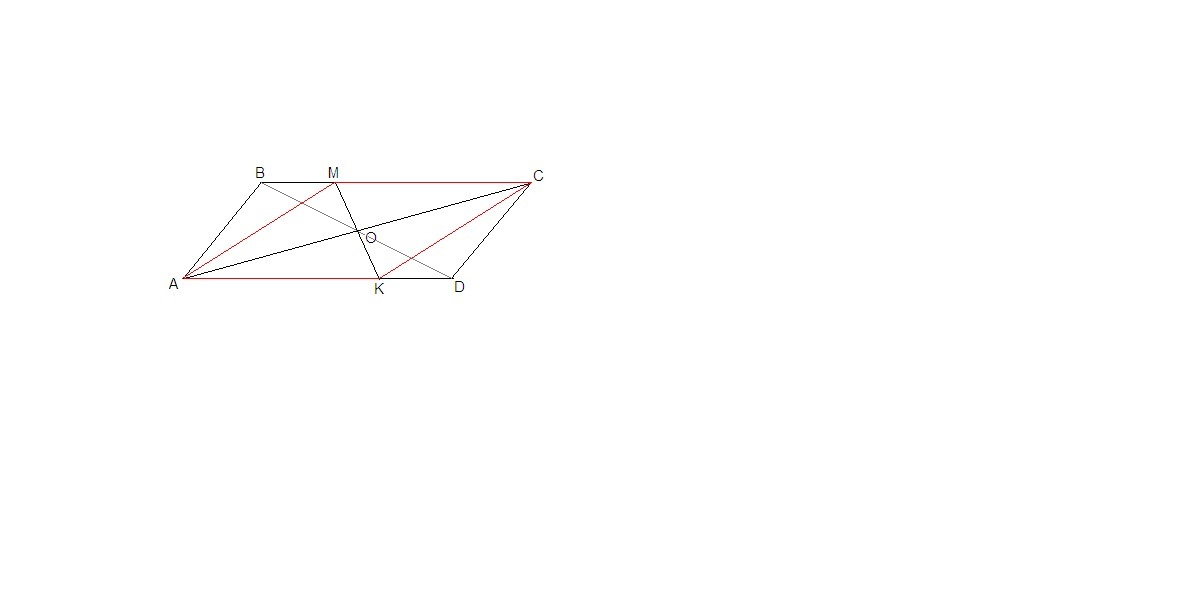
Прямая проходит через середину диагонали AC параллелограма ABCD и пересекает стороны BC и AD в точках M и K соответственно. Доказать: AMCK - параллелограм.
Ответы
Автор ответа:
0
Пусть О - середина АС. Тогда
АО = ОС,
∠ОАК = ∠ОСМ как накрест лежащие при пересечении ВС║AD секущей АС,
∠АОК = ∠СОМ как вертикальные, ⇒
ΔАОК = ΔСОМ по стороне и двум прилежащим к ней углам.
Значит, КО = ОМ.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
КО = ОМ, АО = ОС, ⇒
АМСК - параллелограмм.
АО = ОС,
∠ОАК = ∠ОСМ как накрест лежащие при пересечении ВС║AD секущей АС,
∠АОК = ∠СОМ как вертикальные, ⇒
ΔАОК = ΔСОМ по стороне и двум прилежащим к ней углам.
Значит, КО = ОМ.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
КО = ОМ, АО = ОС, ⇒
АМСК - параллелограмм.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: lelyaolya25
Предмет: Биология,
автор: zhannaid20
Предмет: Английский язык,
автор: smv74
Предмет: Алгебра,
автор: Сюнька