Предмет: Математика,
автор: zum60485
Решите уравнение :
x^4 - 4x^3 - 2x^2 + 12x + 9 = 0
Приложения:
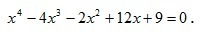
Ответы
Автор ответа:
3
x⁴-4x³-2x²+12x+9=0
(x⁴-4x³+6x²-4x+1)-8x²+16x+8=0
(x-1)⁴-8(x²-2x-1)=0
(x²-2x+1)²-8(x²-2x-1)=0
x²-2x=a
(a+1)²-8(a-1)=0
a²+2a+1-8a+8=0
a²-6a+9=0
(a-3)²=0
a-3=0
a=3
x²-2x-3=0
D=4+12=16=4²
x=(2±4)/2
x1=3
x2=-1
(x⁴-4x³+6x²-4x+1)-8x²+16x+8=0
(x-1)⁴-8(x²-2x-1)=0
(x²-2x+1)²-8(x²-2x-1)=0
x²-2x=a
(a+1)²-8(a-1)=0
a²+2a+1-8a+8=0
a²-6a+9=0
(a-3)²=0
a-3=0
a=3
x²-2x-3=0
D=4+12=16=4²
x=(2±4)/2
x1=3
x2=-1
zum60485:
Cпасибо огромное за старания!
Автор ответа:
5
(x²-2x)² - 6x² +12x+9 =0 ⇔ (x²-2x)² -6(x²-2x) +9 =0 ⇔ ((x²-2x) -3 )² =0 или :
(x²-2x -3 )² = 0 ⇔ x²-2x -3 =0 ⇔ x = 3 или х= -1
Похожие вопросы
Предмет: Українська мова,
автор: oleksandrgoladinec14
Предмет: Литература,
автор: timur10052011
Предмет: Геометрия,
автор: nazarovaksenya220909
Предмет: Информатика,
автор: heavenkenobi
Предмет: Математика,
автор: vasyamynkamvm29