Предмет: Математика,
автор: koljakorovin
найдите область определения выражения 
NNNLLL54:
корень над чем?
Ответы
Автор ответа:
0
спасибо, исправила (палец промахнулся кнопочкой)
Автор ответа:
0
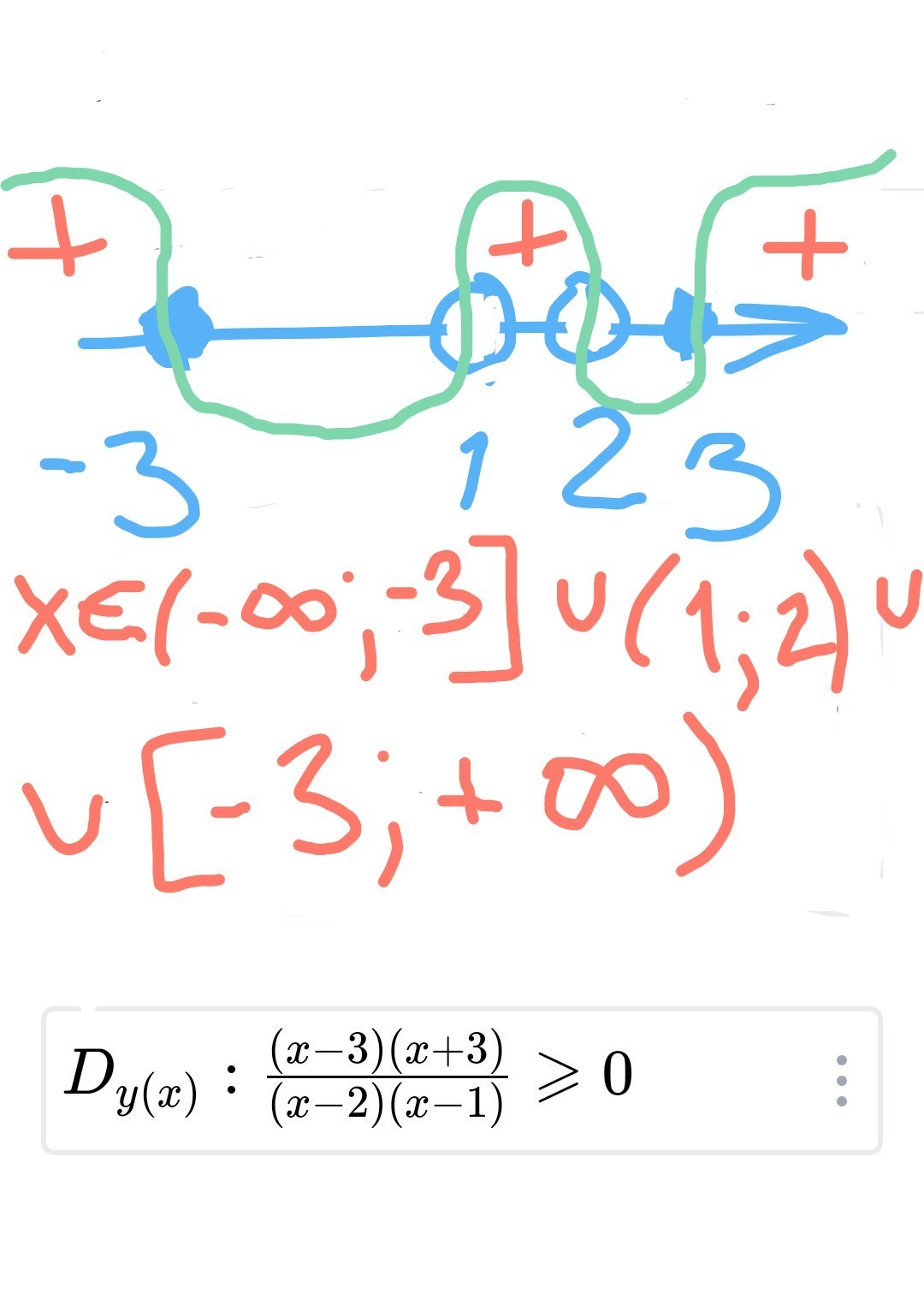
решим методом интервалов
(см рис)
x∈(-∞; -3]∪ (1;2)∪[3;+∞)
это и будет область определения
Приложения:
Похожие вопросы
Предмет: Математика,
автор: reyd7777
Предмет: Қазақ тiлi,
автор: walcket
Предмет: Русский язык,
автор: iiahw
Предмет: Литература,
автор: asdfar2002
Предмет: Математика,
автор: 6543789