Предмет: Математика,
автор: AllegoriaTua
, выручайте! Без Вас никак!
Помогите разобраться в теме, я нахожусь на контрольной, нужно срочно!
Решите и подробно распишите! Быстрее!
Желательно все, точнее умоляю Все решить!
Надеюсь на Вас! Спаси!!!!
Заранее огромное спасибо!
Помоги :)
Приложения:
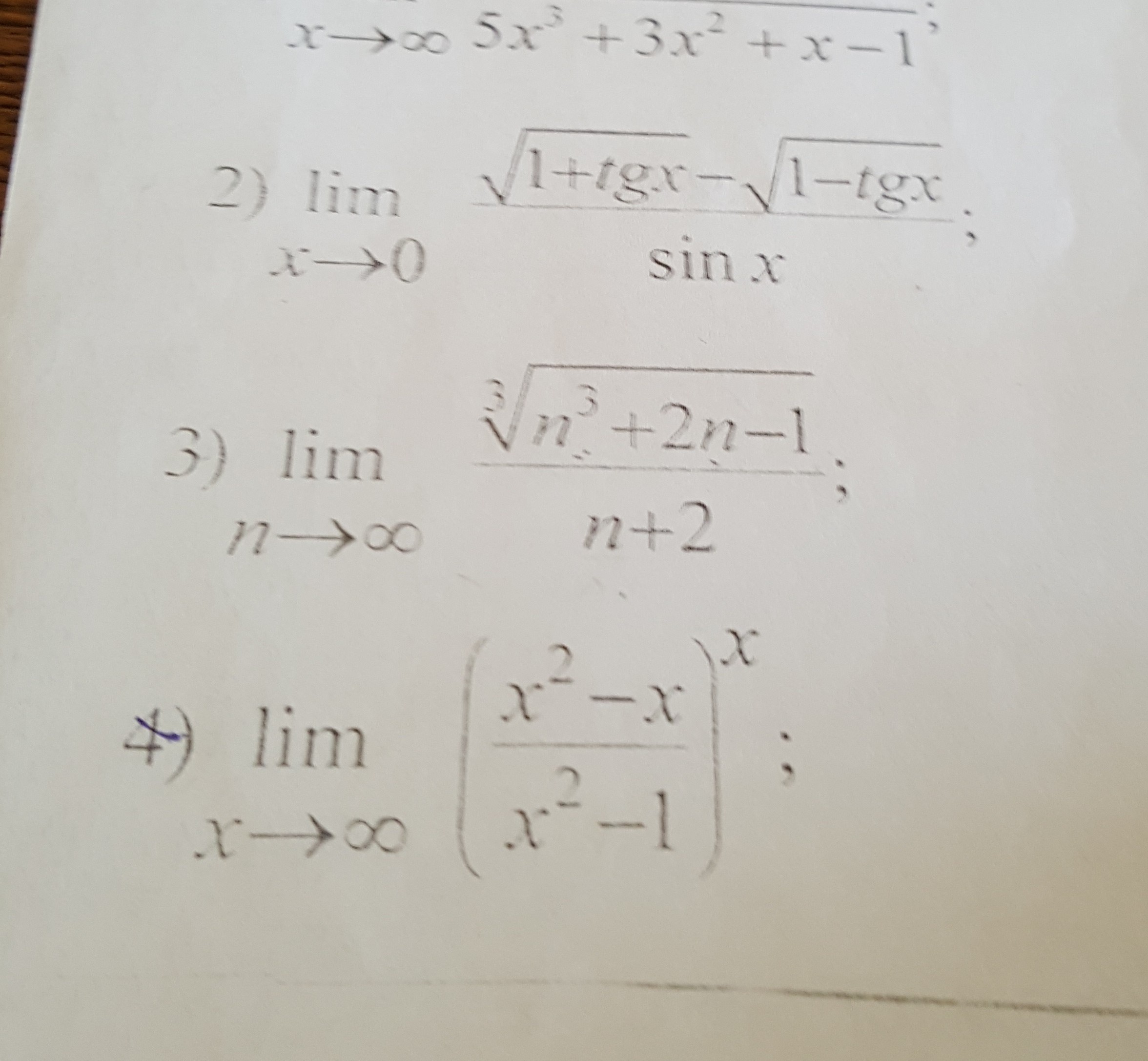
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: narutolove320
Предмет: Русский язык,
автор: leraksaaa
Предмет: Английский язык,
автор: lev228123
Предмет: География,
автор: NEIMAROMEGA
Предмет: История,
автор: kgarajshinа