Предмет: Алгебра,
автор: anastasiamih4
Готова дать 40 баллов, за 3 примера.
Нужно найти производную функции.
Приложения:
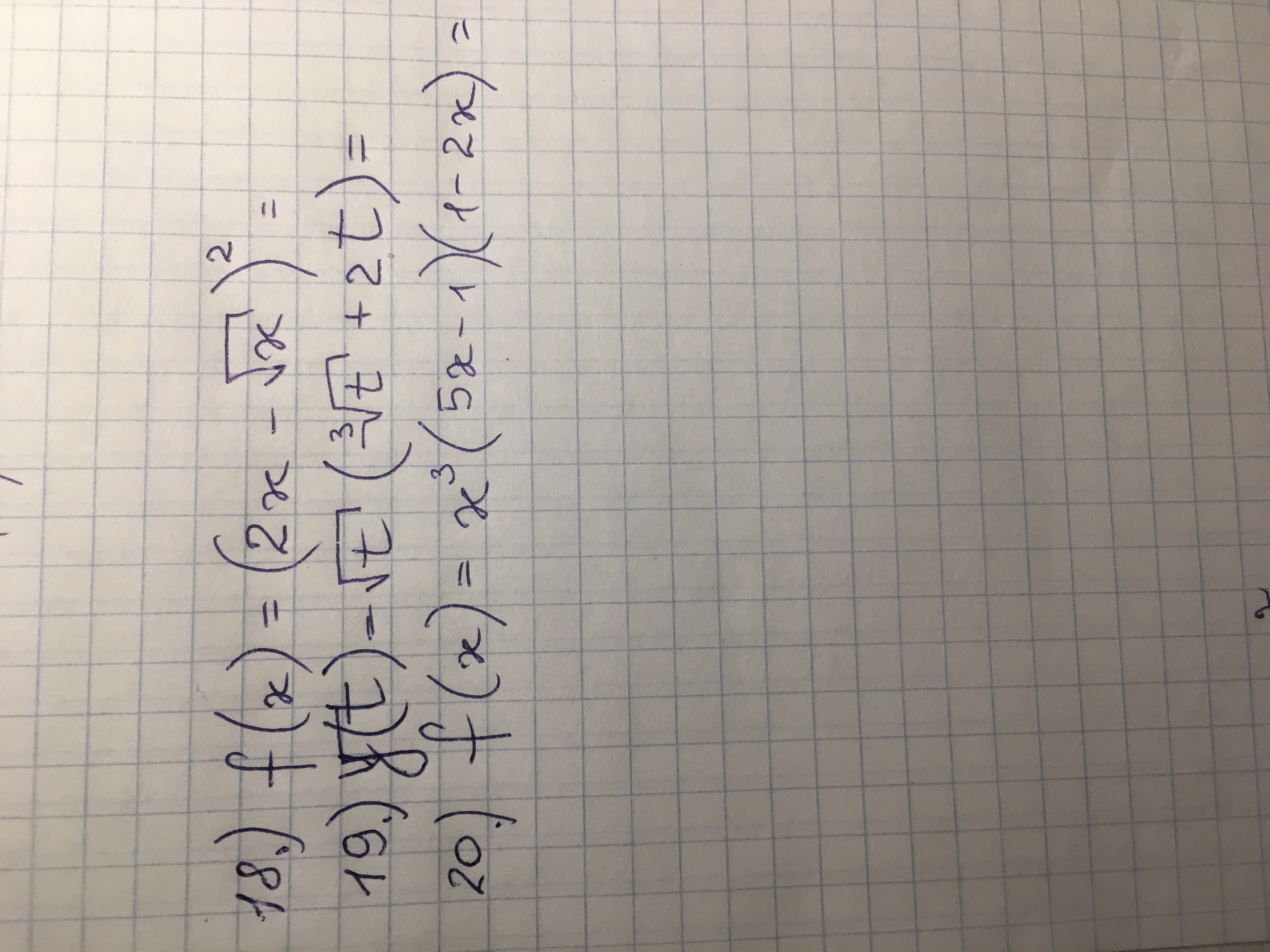
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Биология,
автор: maksikbiloys10765
Предмет: Информатика,
автор: zignifuspe
Предмет: Математика,
автор: butovaagenlinkaasas
Предмет: Литература,
автор: Maha331