Question

Квадроцикл проїхав половину шляху зі швидкістю 50 км/год. Половину часу, який залишився, він їхав зі швидкістю 20 км/год, а решту - зі швидкістю 40 км/год. Визначте середню швидкість руху квадроцикла на всьому шляху.

Answer 1

Квадроцикл проехал половину пути со скоростью 50 км/час. Половину оставшегося времени он ехал со скоростью 20 км/ч, а остальное - со скоростью 40 км/ч. Определите среднюю скорость движения квадроцикла на всем пути.

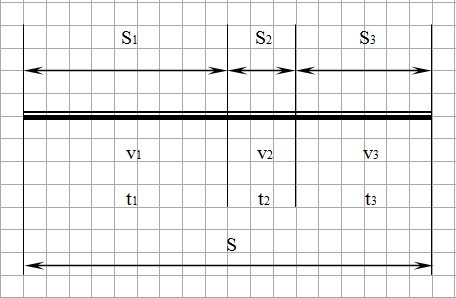
Дано:  S₁ = S/2;   t₂ = t₃;   v₁ = 50 км/ч;   v₂ = 20 км/ч;   v₃ = 40 км/ч;   S₁ = S₂+S₃  

Найти: v(cp.) - ?

Решение:   Запишем все, известное по условию:

                                    S₁ = v₁t₁;   S₂ = v₂t₂;   S₃ = v₃t₃;   S₁ = S₂+S₃;   t₂ = t₃

Средняя скорость равна отношению всего пройденного пути ко всему времени движения:

     

$\displaystyle \tt v_{cp.}=\frac{S_{1}+S_{2}+S_{3}}{t_{1}+t_{2}+t_{3}}=\frac{2S_{1}}{\dfrac{S_{1}}{v_{1}}+\dfrac{(t_{2}+t_{3})(v_{2}+v_{3})}{v_{2}+v_{3}}}=\\\\\\=\dfrac{2S_{1}}{\dfrac{S_{1}}{v_{1}}+\dfrac{t_{2}v_{2}+t_{2}v_{3}+t_{3}v_{2}+t_{3}v_{3}}{v_{2}+v_{3}}}=\frac{2S_{1}}{\dfrac{S_{1}}{v_{1}}+\dfrac{S_{2}+S_{3}+S_{2}+S_{3}}{v_{2}+v_{3}}}=$

$\displaystyle \tt =\frac{2S_{1}}{\dfrac{S_{1}}{v_{1}}+\dfrac{2S_{1}}{v_{2}+v_{3}}}=\frac{2S_{1}}{\dfrac{S_{1}\cdot(v_{2}+v_{3})+2S_{1}v_{1}}{v_{1}\cdot(v_{2}+v_{3})}}=\frac{2v_{1}\cdot(v_{2}+v_{3})}{2v_{1}+v_{2}+v_{3}};\\\\\\v_{cp.}=\frac{2\cdot50\cdot(20+40)}{2\cdot50+20+40}=\frac{6000}{160}=37,5$

---------------------------------

Ответ: 37,5 км/ч