Question

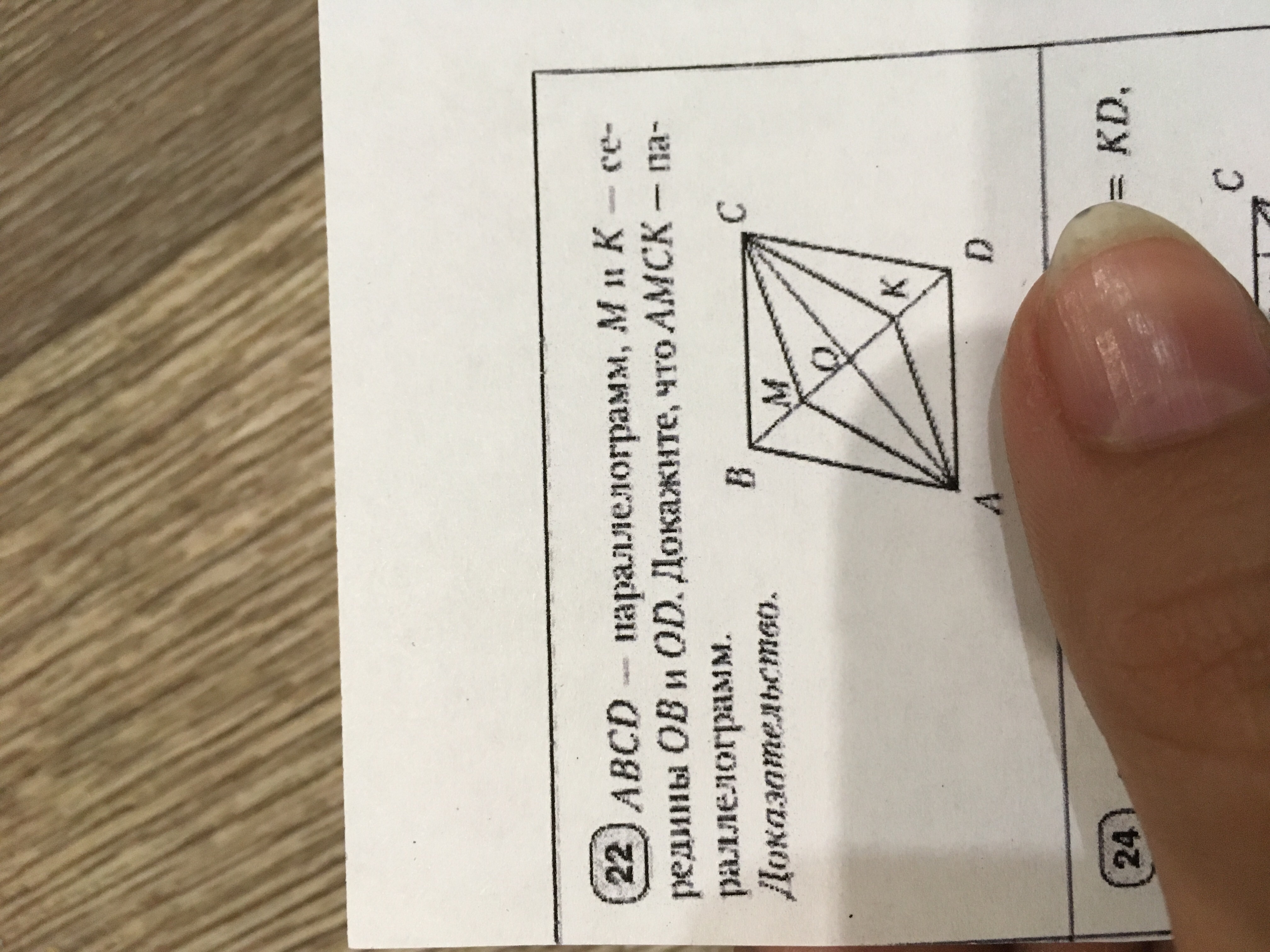
Помогите пожалуйста,срочно

Answer 1

Докозательство:

1. М и К середины ВО и ОD => МО = ОК

2. АО = ОС т.к. о - т. пересечения АС

3. По п. 1 и п. 2 мы можем доказать ,что АМСК - параллелограм по признаку параллелограма

                                                                                              ЧТД

Answer 2

Чтобы решить эту задачу, вспомним теорему: в паралеллограмме диагонали точкой пересечения делятся пополам. Верно и обратное: если в четырёхугольнике диагонали точкой пересечения делятся пополам, то данный четырёхугольник — параллелограмм.

***

В параллелограмме диагонали в точке пересечения делятся пополам, поэтому BO=OD. Поскольку MO и OK равны соответственно половинам отрезков BO и OD, которые равны между собой, то они тоже равны: MO=OK.

Рассмотрим четырёхугольник AMCK. Его диагонали в точке пересечения делятся пополам, а значит, он также является паралеллограмом.

***

Если моё решение оказалось полезным, смело отмечайте его как «лучший ответ».