Предмет: Математика,
автор: vlad0911254
Привет! Помогите пожалуйста найти область определения функции(желательно с фото). Дам 15 баллов.
Приложения:
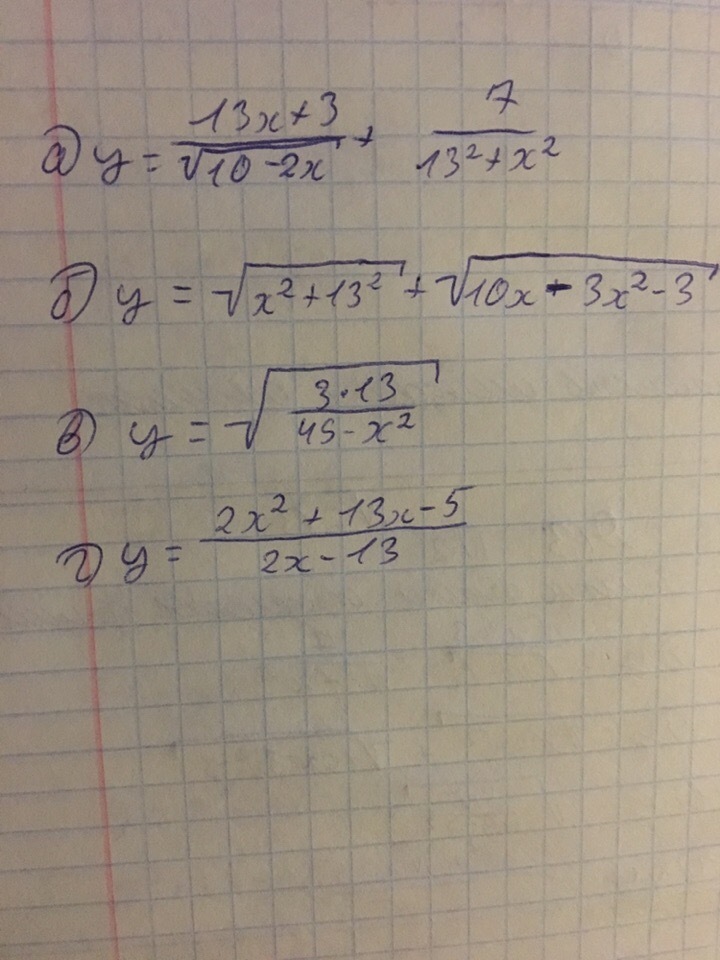
Ответы
Автор ответа:
1
(1)



при любых х
поэтому
Ответ:
область определения
х€( -∞; 5 )
(2)

13²+х²всегда >0

решим



наше неравенство
решаем методом интервалом (см рисунок1)
Ответ:
область определения
x€[ ⅓; 3 ]
(3)


опять прибегаем к методу интервалов
для решения неравенства
см рисунок 2
Ответ:
область определения
x€(-3√5; 3√5)
(4)

2x-13≠0
x≠6,5
Ответ:
область определения
x€(-∞; 6,5) v(6,5; +∞)
при любых х
поэтому
Ответ:
область определения
х€( -∞; 5 )
(2)
13²+х²всегда >0
решим
наше неравенство
решаем методом интервалом (см рисунок1)
Ответ:
область определения
x€[ ⅓; 3 ]
(3)
опять прибегаем к методу интервалов
для решения неравенства
см рисунок 2
Ответ:
область определения
x€(-3√5; 3√5)
(4)
2x-13≠0
x≠6,5
Ответ:
область определения
x€(-∞; 6,5) v(6,5; +∞)
Приложения:
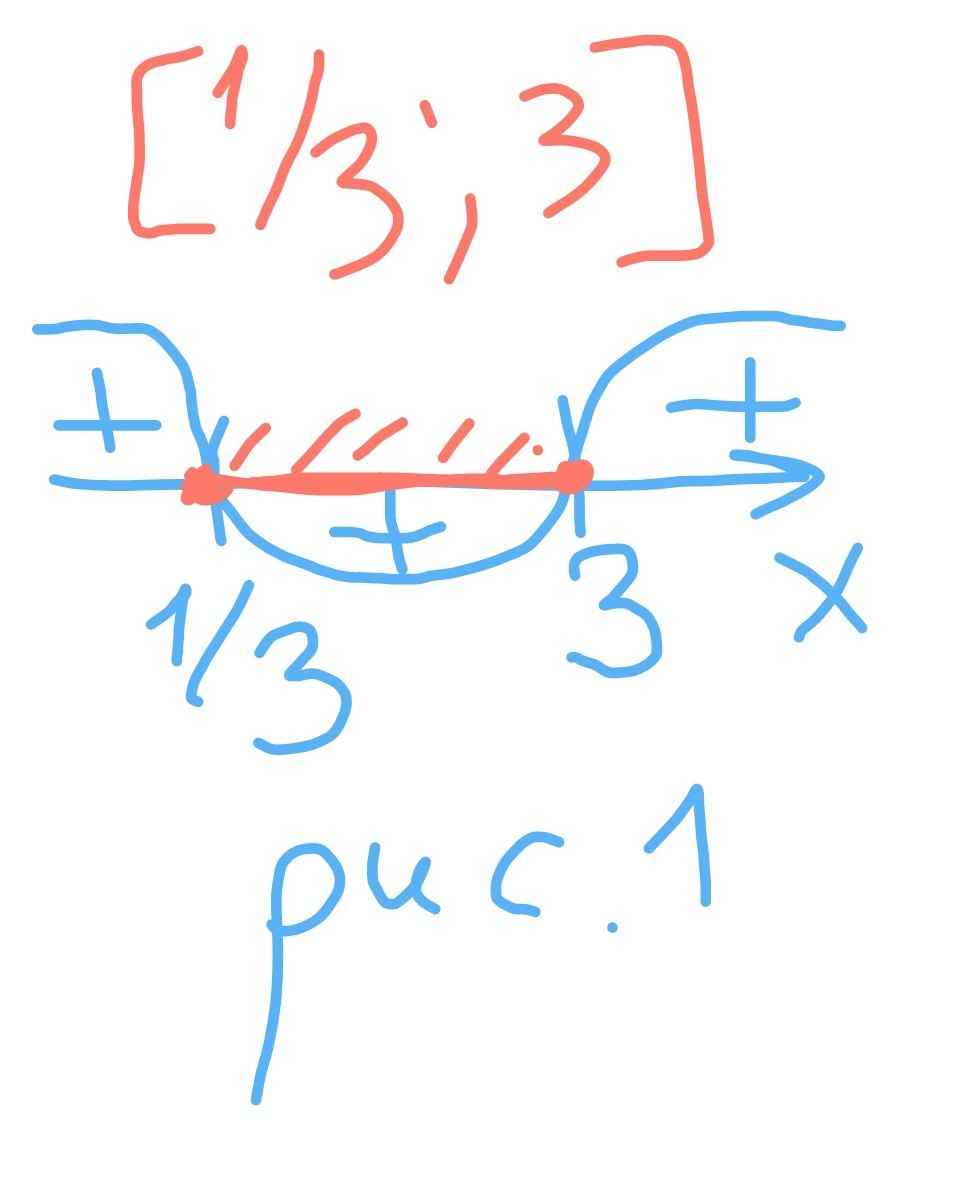
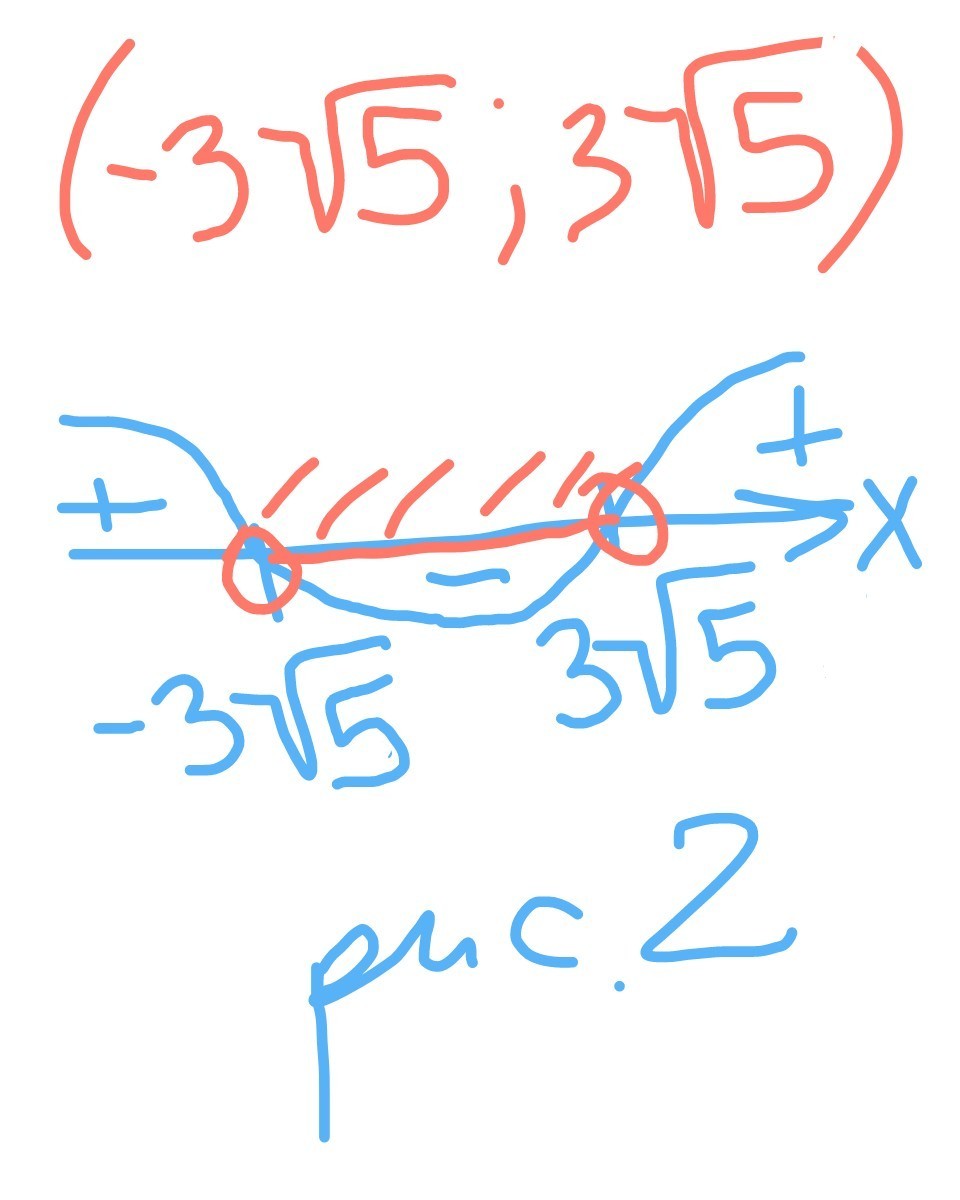
Спасибо большое
Похожие вопросы
Предмет: Геометрия,
автор: nurai300819
Предмет: Математика,
автор: amikooos
Предмет: Химия,
автор: elvinaartemova5
Предмет: Алгебра,
автор: кисазая3
Предмет: Химия,
автор: Альбина6699458823948
Фу́нкция (отображе́ние, опера́тор, преобразова́ние) — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так, значение переменной. однозначно определяет значение выражения.