Предмет: Математика,
автор: golovachevkonstantin
Найти общие решение дифференциальных уравнений
Приложения:
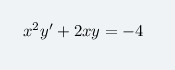
Ответы
Автор ответа:
0
Это линейное неоднородное диффиренциальное уравнение вида
Для начала надо найти решение соотв. однородного дифф-урафнения
Однородное:
Теперь найдём решение неоднородного уравнения:
Представим С как функцию от X.
Подставим в исходное уравнение:
Решение:
Похожие вопросы
Предмет: Физика,
автор: valeriaromanova98
Предмет: Математика,
автор: wkondrashova2000
Предмет: История,
автор: pumpkinnn
Предмет: Математика,
автор: limyruk
Предмет: Информатика,
автор: PoooOOooH