Question

Найдите наименьшее и наибольшее значение функции y=cosx а) на отрезке [π/6;2π/3]
б) на интервале (-π;π/4)
в) на луче [-π/3;+ восьмерка перевернутая)
г) на полуинтервале[-π/3;3π/2)

Answer 1

Объяснение:

а) на отрезке [π/6; 2π/3] cos убывает, а значит наибольшего значения достигает при x = π/6; y = √3/2, а наименьшего при x = 2π/3; y = -1/2

б) наименьшее = -1 (при x = -π), наибольшее = 1 (при x = 0)

в) наименьшее = -1 (в точках x = π + 2πk, k∈Z⁺), наибольшее = 1 (в точках 2πk). Примечание: Z⁺ = N∪{0}

г) наименьшее = -1 (в точке x = π), наибольшее = 1 (в точке x = 0)

Answer 2

Ответ:

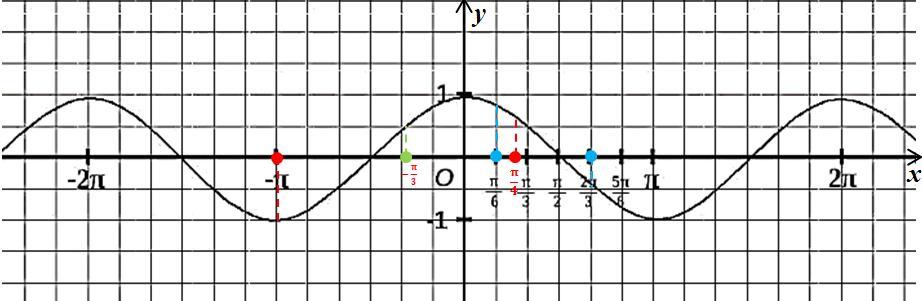
См. рисунок в приложении.

а) На отрезке [π/6; 2·π/3] функция y=cosx убывает, поэтому:

• наибольшего значения достигает в левой границе, то есть при x = π/6: y(π/6)=√3/2;

• наименьшего значения достигает в правой границе, то есть при x = 2·π/3:  y(2·π/3) = -1/2

б) интервал (-π; π/4) содержит значения x=-π и x = 0, в которых функция y=cosx:

• достигает наибольшего значения при x = 0: y(0) = 1;
• достигает наименьшего значения при x = -π: y(-π) = -1;

в) луч [-π/3; +∞) содержит значения x=0 и x = π, в которых функция y=cosx:

• достигает наибольшего значения при x = 0: y(0) = 1;
• достигает наименьшего значения при x = π: y(π) = -1;

г) полуинтервал [-π/3; 3π/2) содержит значения x=0 и x = π, в которых функция y=cosx:

• достигает наибольшего значения при x = 0: y(0) = 1;
• достигает наименьшего значения при x = π: y(π) = -1.