Question

Найдите площадь равнобедренной трапеции, боковая сторона которой равна 5 см, нижнее основание равно 13 см, а верхнее – 7 см.

Answer 1

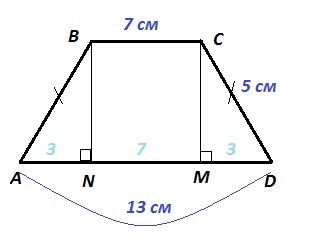
ABCD - равнобедренная трапеция, AB=CD=5 см; BC=7 см; AD=13 см

Опустим две высоты  BN⊥AD  и  CM⊥AD.  

BCMN - прямоугольник  ⇒

NM = BC = 7 см   ⇒    AN = MD = (13-7)/2 = 3 см

ΔCMD - прямоугольный, теорема Пифагора

CM² = CD² - MD² = 5² - 3² = 16 = 4²

CM = 4 см   - высота трапеции

Площадь трапеции

$S=\dfrac{AD+BC}{2}\cdot CM=\dfrac{13+7}{2}\cdot 4=40$  см²

Ответ:  40 см²