Помогите срочноооо!!!!
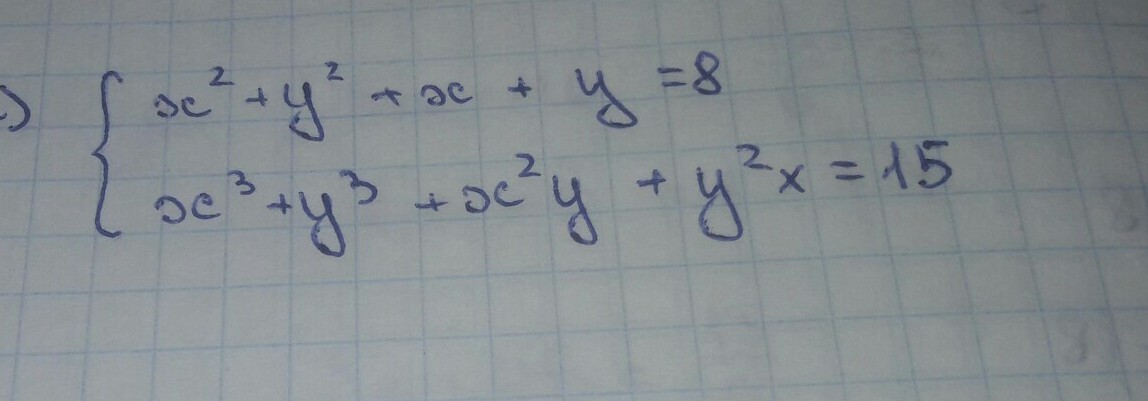
Ответы
task/29846835 Решить систему { x²+y² +x+y =8 ; x³+y³ + x²y+y²x =15 .
Решение: систему перепишем в виде
{ (x+y)² -2xy +(x+y) =8 ; (x+y)³ -3xy(x+y) +xy(x+y) =15.
производя замену: (x+y) =u ; xy = v, получаем { u²-2v +u =8 , u³-2uv =15. ⇔
{ u² -2v = 8 -u ; u(u² -2v) =15. u(8-u) =15 ⇔ u² - 8u +15 = 0 ⇔ [ u =3 ; u= 5.
* * * [x+y =3 ; x+y= 5 * * *
a) u =3 → во второе уравнение : 3(3² -2v) =15⇒v =2. и обратной заменой
{ x+y =3 ; xy =2. x и y можно представлять как корни квадратного уравнения t² -3t +2 =0 (обр.теорема Виета)⇒ [ t=1 ; t=2. ответ а : (1 ;2) , (2;1).
б) u =5 (аналогично) : 5(5²-2v) =15⇒v =11
{ x+y =5 ; xy =11. ⇒t² - 5t +11 = 0 , D = 5²-4*1*11 = -19 <0 не имеет действительных корней .
ответ: (1 ;2) , (2; 1) .