Question

Внутри большего квадрата расположен меньший квадрат площади 89. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?

Answer 1

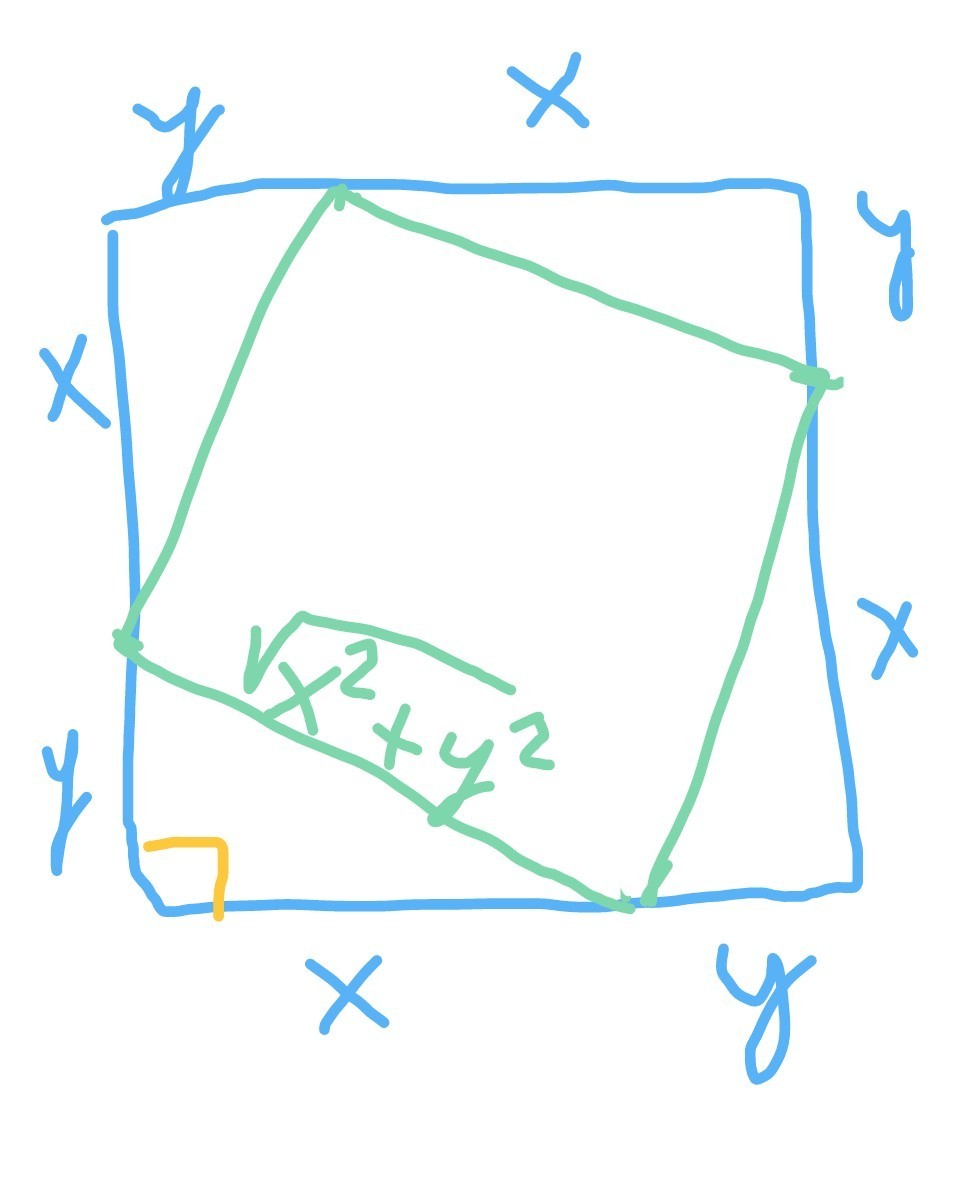
пусть вершины малого квадрата разбивают стороны большого на отрезки длиной х и у
(см рис)

тогда квадрат стороны малого квадрата по теореме Пифагора

${x}^{2} + {y}^{2}$
а это и есть площадь малого квадрата, которая по условию = 89

Получаем уравнение
${x}^{2} + {y}^{2} = 89$

которое надо решить в целых положительных числах

Нетрудно видеть , что решением
являются х=8, у=5 ( или наоборот)

Поэтому площадь большого квадрата
$(x + y) ^{2} = \\ = (8 + 5) ^{2} = (5 + 8) ^{2} = \\ = {13}^{2} = 169$