Предмет: Алгебра,
автор: houussee30
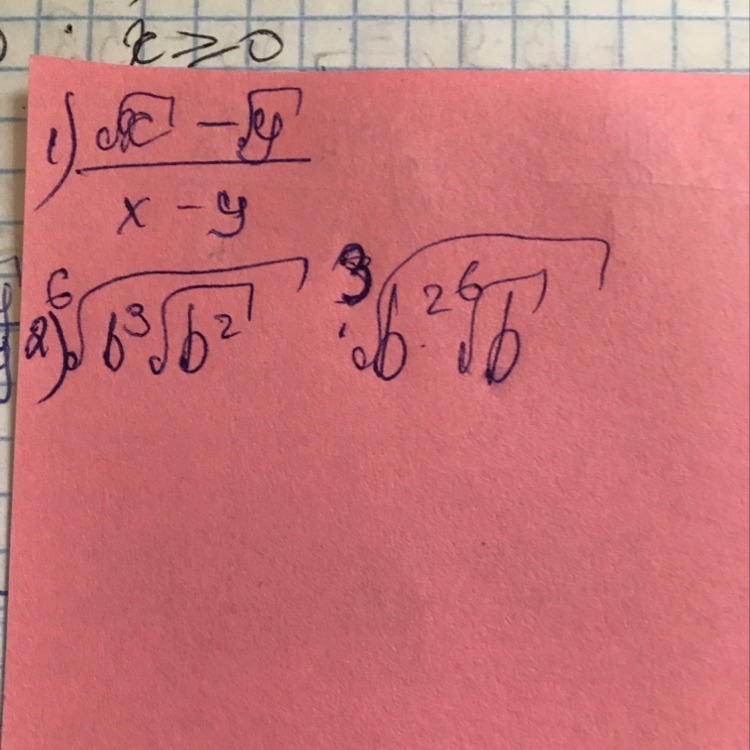
упростите прошууууу
пожалуйста
Приложения:
Ответы
Автор ответа:
1
houussee30:
можно вопрос?
во втором выражении в первом множителе вторая b в квадрате
вы это как-то упростили?
b^2 внесли под корень 6 степени, и там она превратилась в b^{12}
а, всё понятно, огромное спасибо, вы мне очень помогли
Дописала преобразования...
Похожие вопросы
Предмет: Психология,
автор: Аноним
Предмет: Математика,
автор: podkovirovm
Предмет: Английский язык,
автор: dilsodova06
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: VoLcHica2004